Prawdopodobienstwo Marcinek: Witam, prosze o jaką podpowiedz jak zaczac zadanie: Z przedziału (0,1] wybrano dwie liczby: x i y. Znaleźć prawdopodobieństwo tego, że iloraz drugiej przez pierwszą nie przekroczy 3, ale jest większy niż 1. Czyli zdarzenie A − 1 < ^x_y < 3 Proszę o jakieś wskazówki jak ruszyć te zadanie. Czy to jest prawdopodieństwo warunkowe? Z góry dzięki za każde podpowiedzi!

Marcinek:

	y
Wyżej jest pomyłka, powinno być: zdarzenie A − 1 <		< 3
	x

Sabin: Z Twojego zapisu wynika, że y > ^x₃ oraz y < x. Narysuj układ i policz p−two jako pole tego obszaru do pola całości.

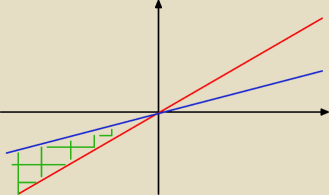
Marcinek: Nie wiem czy dobrze zrozumiałem. Dla y>x i y<3x wyszedł mi mniej więcej taki wykres. Jak policzyć prawdopodobieństwo jako pole tego obszaru do pola całości?

Sabin: Prawie, ograniczasz się do obszaru kwadratu − zgodnie z przedziałem który masz podany w zadaniu. Wtedy p−two liczysz jako pole zakreskowanej figury (trójkąta − metoda dowolna) do pola kwadratu.

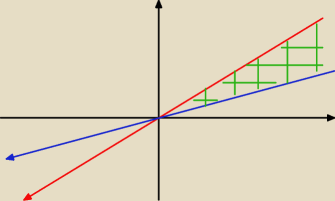
Marcinek: Fakt, dzięki, moje przeoczenie. Czyli wyjdzie coś takiego? Pole kwadratu w takim razie będzie wynosiło 1² Tylko jak obliczyć pole takiego trójkąta?

Sabin: No jakoś tak będzie, choć ja bym był trochę dokładniejszy przy rysunku. Dalej wyznaczasz punkty przecięcia się prostych z prostą y = 1, liczysz podstawę (tak jakby stawiając trójkąt do góry nogami), wysokość = 1.

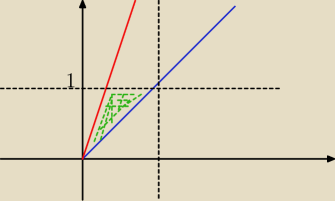
Sabin: Jakos tak

Marcinek: Czyli podstawa będzie miała długość 1−0,33 = 0,77? W takim razie pole trójkąta będzie równało się 0,5 * 0,77 * = 0,385

Sabin: Nie, jeśli już to podstawa ma długość 1 − 1/3 = 2/3 − nie przybliżaj w taki sposób (jeszcze z błędem) Stąd pole = 1/2 * 2/3 * 1 = 1/3 A stąd p−two = 1/3 : 1 = 1/3

Marcinek: Faktycznie! Dziękuje Ci bardzo Sabin, na prawdę mi pomogłeś! Pozdrawiam serdecznie!

Sabin: Damy radę Wzajemnie.