zestaw rozszerzony Karola: wiedząc, że w trójkącie ABC zachodzi związek |BC|=√2*|AC|, sprawdź, czy zachodzi równość: cos²α=cos2β

Jack: pewnie zależy gdzie rozmieścisz te kąty w trójkącie..

Karola: dużo mi nie pomogłeś

Jack: przydałby się informacja o tych kątach np w postaci rysunku. Przypuszczam że odpowiedź na pytanie zależy od rozmieszczenie kątów.

Karola: nie mam żadnego rysunku w zadaniu myśle że to może być tak

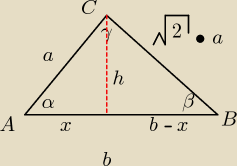
Jack: Teza: cos²α=cos2β cos2β=cos²β−sin²β Z rys. cosα=h/a ⇒ cos²α=x²/a²

	b−x		(b−x)2
cosβ=		⇒ cos2β=
	√2a		2a2

sinβ=h/√2a ⇒ cos²β=h²/2a² oraz (b−x)²=2a²−h² (z tw. Pit.)

	h2/2a2		h2
stąd: cos2β=		=
	2a2		2a4

Liczymy:

	h2		h2		h2(1−2a2)
cos2β−sin2β=		−		=
	2a4		2a2		2a4

	x2		2a2(a2−h2)
cos2α=		=
	a2		2a4

sprawdź sobie czy zachodzi równość...