Trapez Dex: Zostało mi ostatnie zadanie z arkusza, dodatkowo z tematu którego nie znoszę i jestem z niego tępy. Proszę o pomoc Punkt E leży na ramieniu BC trapezu ABCD, w którym AB || CD. Udowodnij, że |<) AED| =|<) BAE| + |<) CDE|. Znalazłem rozwiązanie na innej stronie, ale niewiele z niego łapię. http://www.zadania.info/771471 Proszę o jakieś naprowadzenie.

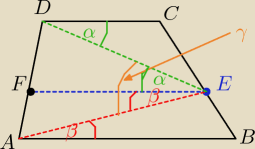
Eta: Odcinek FE II AB i II DC podzielił trapez ABCD na dwa trapezy: ABEF i FECD Kąty "α" w trapezie FECD są naprzemianległe, to ich miary są równe podobnie, kąty "β" w trapezie ABEF zatem miara kąta γ= α+β co oznacza równość: |<AED|= |<BAE| + |<CDE| co kończy dowód