:) M4ciek: Wyznacz te wartosci parametru m , dla ktorych rownanie :

	m2 − 4m − 4
cos x =
	m2 + 1

	π
ma rozwiazanie nalezace do przedzialu (0,		).
	3

Prosze o pomoc

Eta:

	π		1
cos		=
	3		2

cos0= 1 rozwiąż układ nierówności

	m2−4m−4
		>1
	m2+1

	m2−4m−4		1
i		<
	m2+1		2

M4ciek: Ok , dzieki

:]: ten uklad nie ma rozwiazania jak cos moze byc wieksze od 1 i jednoczesnie mniejsze od 1/2

M4ciek: Hmm wiec co teraz

:]: Machnela sie Eta odwrotnie >0,5 a <1

ICSP:

	1
według mnie znaki powinny być na odwrót <1 oraz drugi >
	2

Eta: No wiadomo,"machnęła się Eta" w zapisie , bo była głodna

Eta:

Godzio: na małego głoda

Eta: He he.... właśnie zjadłam budyń z sokiem malinowym

Godzio: To ja idę po moje podusiaki (płatki jakby ktoś nie wiedzial )

Eta: Wiem, wiem .....jadam je na śniadanko + magusie+ kangusy

Godzio:

Eta:

M4ciek: Czy ja tutaj mam gdzies blad bo juz dzisiaj wszystko mieszam :

m2 − 4m − 4		1
	>
m2 + 1		2

2m2 − 8m − 8 − 1
	> 0 / (2m2 + 2)2
2m2 + 2

(2m² − 8m − 9) * ( 2m² + 2) > 0 m₁ = − 1 v m₂ = 9 m ∊ (−∞,−1) ∪ (9,+∞)

m2 − 4m − 4
	< 1
m2 + 1

m2 − 4m − 4 − m2 − 1
	< 0 /*(m2 + 1)2
m2 + 1

(−4m − 5) * (m² + 1) < 0

	5
m =		, a > 0
	4

m ∊∅ I ∩ II = m ∊ (−∞,−1) ∪ (9,+∞)

Godzio: Tak i to na samym początku

M4ciek: Gdzie na poczatkuPrzenioslem na druga strone i do wspolnego mianownika

Eta: nie pomnożyłeś −1( m²+1)

Godzio:

m2 − 4m − 4		1
	>
m2 + 1		2

m2 − 4m − 4		1
	−		> 0
m2 + 1		2

2m2 − 8m − 8 − (m2 + 1)
	> 0 / * (2m2 + 2) bo 2m2 + 2 > 0
2m2 + 2

m² − 8m − 9 > 0 (m − 9)(m + 1) > 0 m ∊ (−∞,−1) ∪ (9,∞)

m2 − 4m − 4
	< 1
m2 + 1

m² − 4m − 4 < m² + 1 −4m < 5

	4
m > −
	5

	4
Odp: m ∊ (−		, −1) ∪ (9,∞)
	5

Eta:

M4ciek: Wrrr to po probnej maturze tak Kazde wytlumaczenie jest dobre

Godzio: Fajnie że ja miałem jakąś próbną maturę prócz tej z listopada ...

M4ciek: Potrzebna Ci jest

Godzio: No przydałoby się sprawdzić jak by mi poszło z rozszerzenia

M4ciek: Godziu −4m < 5 / : (−4)

	5
m > −
	4

Godzio: O to mi właśnie chodziło

M4ciek: Specjalnie to napisales

Godzio: Omyłkowo

M4ciek: Myslalem ,ze specjalnie ,zeby bez sensu nie spisal

Godzio: Czy ktoś spisuje czy analizuje to już jego sprawa, ja jedynie co mogę to rozwiązać i w miarę możliwości wytłumaczyć

M4ciek:

Eta: No to zad. dla Godzia na dobranoc ( przed zaśnięciem) zad1/ ( 5pkt) Dane są zdarzenia A i B, zawarte w Ω i takie ,że P(A U B)=0,9 , P(A∩B)= 0,3 , P(A U B^') =0,5 Wyznacz: P(A^' U B)

Eta: Zad2/ (5pkt) W trójkącie równoramiennym ABC , gdzie |AB|= |BC| i o podstawie długości 6 Punkt P jest punktem przecięcia wysokości poprowadzonych z wierzchołków A i B. Oblicz pole trójkąta ABC, jeżeli |PC|= 4

Godzio: Eta pozwolisz sobie że 1 sobie odpuszczę, bo to akurat banał który już 100 razy robiłem, może M4aciek się skusi Drugie za moment

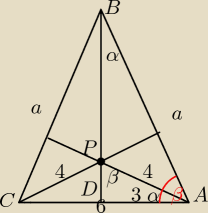
Godzio: Z podobieństwa: ADP ~ ABD :

4		√7		12		12√7
	=		⇒ a =		=
a		3		√7		7

3		√7		9√7
	=		⇒ h =
h		3		7

	ah		12 * 9 * 7		54
P =		=		=
	2		7 * 7 * 2		7

Eta: He he Mimo wszystko jestem bardzo ciekawa bo z tym "banałem" można jechać ..... " z Gdańska do Sopotu przez np. Londyn"

Godzio: No to jeszcze jakoś dam radę, mam nadzieję że o Afrykę nie zahaczę

Godzio: zad1/ ( 5pkt) Dane są zdarzenia A i B, zawarte w Ω i takie ,że P(A U B)=0,9 , P(A∩B)= 0,3 , P(A U B') =0,5 Wyznacz: P(A' U B) P(A'∪B) = P(A') + P(B) − P(A'∩B) = P(A') + P(B) − (P(B) − P(A∩B) ) = P(A') − P(A∩B) = 1 − P(A) − P(A∩B) = 0,7 − P(A) P(A) + P(B) = P(A U B) + P(A∩B) = 1,2 P(A U B') = P(A) + P(B') − P(A∩B') = P(A) + P(B') − (P(A) − P(A∩B)) = 1 − P(B) + 0,3 = 1,3 − P(B) 1,3 − P(B) = 0,5 ⇒ P(B) = 0,8 P(A) + P(B) = 1,2 ⇒ P(A) = 0,4 P(A'∪B) = 0,7 − 0,4 = 0,3 I jak, wydaje mi się że jednak trochę na około poleciałem

Eta: W zad2/ wynik nie zgadza z Twoim

	27√7
P=
	7

Eta: zad1/ odp: 0,9

Godzio: No tak, bo Godzio potraktował "a" jako podstawę

	6 * h		9√7		27√7
P =		= 3 *		=
	2		7		7

Godzio: No to fajnie wszystko źle, znajdę błąd i idę spać

Eta:

Godzio: Już znalazłem, P(A'∪B) = P(A') + P(B) − P(A'∩B) = P(A') + P(B) − (P(B) − P(A∩B) ) = P(A') + P(A∩B) = 1 − P(A) − P(A∩B) = 1,3 − P(A) P(A) + P(B) = P(A U B) + P(A∩B) = 1,2 P(A U B') = P(A) + P(B') − P(A∩B') = P(A) + P(B') − (P(A) − P(A∩B)) = 1 − P(B) + 0,3 = 1,3 − P(B) 1,3 − P(B) = 0,5 ⇒ P(B) = 0,8 P(A) + P(B) = 1,2 ⇒ P(A) = 0,4 P(A'∪B) = 1,3 − 0,4 = 0,9

Godzio: A masz może jeszcze coś ? W sumie mam jutro 2 matmy pierwsze, a skoro i tak się nudze to ...

Eta: 1) A U B^'= (AnB) U B^' , 2) A^' UB= (AnB)U A^' 1) 0,5= 0,3+P(B^') => P(B^')= 0,2 => P(B)= 0,8 2) P(A^'UB)= 0,3 +1− P(A)= 1,3− P(A) P(AUB) = P(A) +P(B) − P(AnB) 0,9 = P(A) +0,8 −0,3 => P(A)= 0,4 to: P(A^'UB)= 1,3−0,4= 0,9 myślę,że nieco krócej

Godzio : Ano trochę tak

Eta: Godzio Jutro coś Ci podrzucę, bo już jestem padnięta Dobranoc, miłych snów

Godzio : Ok Dobranoc