 2x−3y+18=0
3y=2x+18
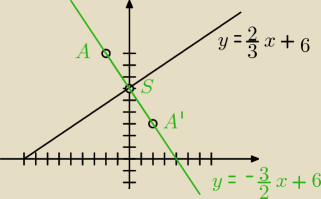
y = 23x + 6
a = 23
a1 = −32
y = −32(x+2)+9
y = −32x + 6y32x6 → prosta prostopadła przechodząca przez punkt
A
szukamy punktu S, w którym proste się przetną
23x + 6 = −32x + 6
−13x = 0
x = 0
y = 6
S = ( 0, 6)
Punkt S będzie środkiem odcinka |AA'|
S = (xS, yS)
2x−3y+18=0
3y=2x+18
y = 23x + 6
a = 23
a1 = −32
y = −32(x+2)+9
y = −32x + 6y32x6 → prosta prostopadła przechodząca przez punkt
A
szukamy punktu S, w którym proste się przetną
23x + 6 = −32x + 6
−13x = 0
x = 0
y = 6
S = ( 0, 6)
Punkt S będzie środkiem odcinka |AA'|
S = (xS, yS)
| xA+xA' | yA+yA' | |||
S = ( | , | )
| ||
| 2 | 2 |
| −2+xA' | |
= 0 → xA' = 2
| |
| 2 |
| 9+yA' | |
= 6 → yA' = 3
| |
| 2 |