planimetria
ICSP: ABCD to romb.
Szukamy pola tego rombu mają dane:
|DE| =
√313
Nie mam pomysłu jak sie za to zabrać. Może jakąś wskazówkę dostanę?
Zaraz dodam rysunek.
21 mar 21:34
ICSP:
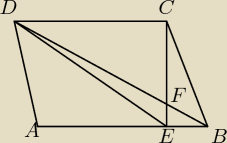
21 mar 21:38
Artur. : DFC jest podobny do EFB? tylko czy coś nam to daje ?


21 mar 21:40
ICSP: Chyba coś daje

Widziałem inne dwa trójkąty podobne ale to może umożliwi mi ułozenie układu
równań z dwoma twierdzeniami Pitagorasa.
21 mar 21:42
ICSP: Chyba jednak nadal czegoś brakuje.
21 mar 21:45
ICSP: Nie ważne już zrobiłem. Dzięki Artur za pomoc

21 mar 22:01
Artur. : yy a podzielisz sie?

21 mar 22:04
Eta:
P= 156 [j
2]

21 mar 22:08
Artur. : A jak do tego dojść?

21 mar 22:09
ICSP: zaraz ci to napisze

21 mar 22:10
Eta:
Z podobieństwa trójkątów i z tw. Pitagorasa

21 mar 22:11
ICSP: DC = 13y
CF = 13x
EF = 5x
EB = 5y
Układasz teraz ukłąd równań z dwoma twierdzeniami pitagorasa i otrzymujesz:
y = 1
P = 13y * 18x
Witaj
Eto masz teraz chwilkę czasu bo mam jeszcze jedno zadanko.
21 mar 22:14
Eta:
Witam

Napisz treść zadania, na chwilkę idę coś zjeść


dla Ciebie
21 mar 22:20
ICSP: Udowodnij że w ciagu geometrycznym o wyrazach dodatnich iloczyn k początkowych wyrazów ciągu
(k∊N, k>1) wyraża się wzorem I ; √(a1ak)k.
21 mar 22:28
Godzio:
Pozwolę sobie pyknąć to zadanko

a
1 * a
2 * a
3 * ... * a
k = a
1k * q
1 + 2 + 3 + ... + (k − 1) = a
1k * q
k(k − 1)2 =
= a
1k/2 * a
1k/2 * (q
(k − 1)/2)
k =
√a1k * (a1 * qk − 1)k =
=
√(a1 * ak)k
21 mar 22:35
ICSP: Dziekuję Godziu
21 mar 22:41
Eta:
W nagrodę ....
Godzia 
21 mar 22:42
Godzio: 
21 mar 22:46



 Widziałem inne dwa trójkąty podobne ale to może umożliwi mi ułozenie układu
równań z dwoma twierdzeniami Pitagorasa.
Widziałem inne dwa trójkąty podobne ale to może umożliwi mi ułozenie układu
równań z dwoma twierdzeniami Pitagorasa.






 Napisz treść zadania, na chwilkę idę coś zjeść
Napisz treść zadania, na chwilkę idę coś zjeść 
 dla Ciebie
dla Ciebie
 a1 * a2 * a3 * ... * ak = a1k * q1 + 2 + 3 + ... + (k − 1) = a1k * qk(k − 1)2 =
= a1k/2 * a1k/2 * (q(k − 1)/2)k = √a1k * (a1 * qk − 1)k =
= √(a1 * ak)k
a1 * a2 * a3 * ... * ak = a1k * q1 + 2 + 3 + ... + (k − 1) = a1k * qk(k − 1)2 =
= a1k/2 * a1k/2 * (q(k − 1)/2)k = √a1k * (a1 * qk − 1)k =
= √(a1 * ak)k

