równanie okregu opisanego na kwadracie
hel me: Napisz równanie okręgu opisanego na kwadracie ABCD wiedząc że B(4;−1) i D(−2;1)
20 mar 21:40
morfepl: wyznacz pozostałe współrzędne kwadratu, następnie policz r, podstaw do wzoru jeden wierzchołek,
potem drugi i otrzymasz układ równań który tylko trzeba rozwiązać
(x−x0)2+(y−y0)2=r2 gdzie środek okręgu O=(x0;y0)
20 mar 21:44
hel me: ojoj a jasniej
20 mar 21:45
morfepl: dobra to najpierw rysunek
20 mar 21:51
hel me: maskra ja wogóle tego nie umiem zadania
20 mar 21:53
morfepl:
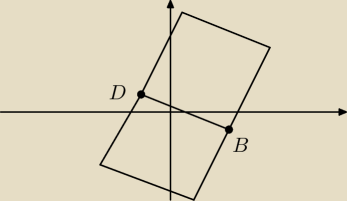
dobra ostro pokraczne ale to nie ważne bo:
okrąg opisany na kwadracie ma promień równy
12d kwadratu
d=a
√2
a=|BD|=
√(4−(−2))2+(−1−1)2=
√36+4=2
√10
r=2
√5
teraz rozwiązujesz układ równań
(4−x
0)
2+(−1−y
0)
2=(2
√5)
2
(−2−x
0)
2+(1−y
0)
2=(2
√5)
2
20 mar 21:59
hel me: ten układ równan tez skomplikowany
20 mar 22:01
morfepl: to nie jedyna opcja, ale byś się musiał bawić w wyznaczenie jakoś wsp pozostałych boków,
dodatkowo zauważyłem kolejny kwadrat o r=√10 więc trzeba rozwiązać jeszcze takie równanie:
(4−x0)2+(−1−y0)2=(√10)2
(−2−x0)2+(1−y0)2=(√10)2
20 mar 22:14
hel me: kurcze
20 mar 22:15