:) M4ciek: Udowodnij tozsamosc :

1 − sin2x		1 − tgx
	=
cos2x		1 + tgx

	sinx   1 −   cosx
P =
	sinx   1 +   cosx

	cosx − sinx   cosx
P =
	cosx + sinx   cosx

	cosx − sinx
P =		/2
	cosx + sinx

	cos2x − 2sinxcosx + sin2x
P =
	cos2x + 2sinxcosx + sin2x

	1 − sin2x
P =
	1 + sin2x

Licznik pasuje , ale co zrobic z tym mianownikem Juz nie mam pomyslow , moze ktos pomoze

Eta: Witam 1= sin²α+cos²α , sin2α= 2sinα*cosα, cos2α= cos²α− sin²α i do dzieła

	sin2α−2sinα*cosα+ cos2α
L=
	cos2α− sin2α

	(cosα− sinα)2
L=
	(cosα−sinα)(cosα+sinα)

	cosα−sinα
L=
	cosα+ sinα

	cosα−sinα   cosα
L=
	cosα+sinα   cosα

	1 −tgα
L=
	1+tgα

L= P , dla cosα≠0

M4ciek: A probowalem od tej strony , ale zle sobie zapisalem Bo zrobilem :

	(sinα − cosα)2
L =
	(cosα − sinα)(cosα + sinα)

I nie udalo mi sie skrocic

Amaz: wymnoz na krzyż i porównaj sobie strony

Eta:

	cosα−sinα   cosα
P=
	cosα+sinα   cosα

	cosα− sinα
P=
	cosα+sinα

	(cosα− sinα)(cosα−sinα)
P=
	(cosα+sinα)(cosα−sinα)

	cos2α+sin2α− 2sinα*cosα
P=
	cos2α− sin2α

	1 −2sinα*cosα
P=
	cos2α

	1 −sin2α
P=
	cos2α

L=P , dla cosα≠0 i sinα≠0 ( zapomniałam napisać ,to drugie założenie Pozdrawiam

Eta: @ Amaz Wykazując tożsamość nie możemy mnożyć "na krzyż"

M4ciek: Dziekuje Eta to jak juz jestes to mi powiesz czy to tak ma byc zaraz cos wkleje

M4ciek: Suma dlugosci wysokosci podstawy i wysokosci sciany bocznej ostroslupa prawidlowego trojkatnego jest rowna 2.Wyznacz dlugosc krawedzi podstawy tego ostroslupa, dla ktorej ma on najwieksze pole powierzchni calkowitej. Zaraz napisze co mam

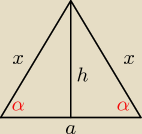M4ciek: Sciana boczna jest Δ rownoramiennym wiec :

	h
tg α =
	1   a 2

	2h
tg α =
	a

	tg α*a
h =
	2

h_sciany + h_podstawy = 2

tg α*a		a√3
	+		= 2
2		2

tg α * a + a√3 = 4 a = ... P_c = Pp + Pb

	a2√3		1		tg α*a
Pc =		+ 3*		a *
	4		2		2

I wlasnie nie wiem co tu zrobic z tym

Eta: To typowe zadanie optymalizacyjne

	a√3
hp=
	2

	a√3
z warunku zad.		+hb= 2
	2

to:

	a√3		4−a√3
hb= 2 −		=
	2		2

	a2√3		a*hb
Pc=		+ 3*
	4		2

podstawiając za h_b, otrzymasz funkcję kwadratową ze zmienną "a"

	√3
P(a)= −		*a2 + 3*a
	4

parabola ramionami do dołu, więc osiaga max w wierzchołku

	−3
dla amax=		=........... = 2√3
	−√3   2*(   4

sprawdź dokładnie rachunki, bo liczyłam "na pichotę"

Eta: "piechotę"

M4ciek: Mi wyszlo √3 i taka jest odp. to pewnie jakis maly chochlik gdzies Dziekuje bardzo

Eta: No tak, powinno być:

	a2√3
P(a)= −		+ 3a
	2

	3
amax=		= √3
	√3