Oblicz R
Trox:
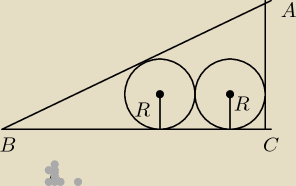
|AC| = 3
|BC| = 4
Oblicz R
Ten trójkąt jest prostokątny, a okręgi takie same.
19 mar 16:31
Trox: Może ktoś jednak da radę?

19 mar 17:44
Kox: masz odpowiedź do tego zadania?
19 mar 20:21
Trox: Nie mam.
23 mar 11:46
komentator OWMH:
Wiem jak to robić; mam problem z rysowaniem na tej strony;
spróbuję tłumaczyć bez rysunku:
oznaczenie:
1.− Niech środek okręgu z lewej strony nazywamy O1 ; Niech M oznacza punkt styczności
tego okręgu z bokiem AB; oraz P oznacza punkt styczności tego okręgu z bokiem BC
2.− Niech środek okregu z prawejjstrony nazywamy O2; oraz T oznacza punkt styczności
tego okręgu z bokiem AC.
dla nas potrzebny będą trzy trójkąty prostokątne:
i) △ prostokątny ACB; gdzie IBCI2 + IACI2 = IABI2
stąd dane są IBCI=4 ; IACI=3 a więc IABI = 5
ii) △ prostokątny ATO2; gdzie ITO1I2 ITAI2= IAO1 I2
ITAI = 3−R ; ITO1I = 3R (bo czworokąt PCTO1 jest prostokąt)
stąd w tym trójkącie mamy: IAO1 I2 = (3−R)2 + (3R)2 .........(α)
iii) △ prostokątny AMO1; gdzie IAM I2 + IMO1I2 = IAO1I2
gdzie IMO1I = R ;
oraz mamy że IAMI = 5−( 4−3R) ⇔ IAMI = 1+3R
(ponieważ IBPI= IBMI odcinki styczne do okręgu; to wynika z tego że
△ BMO1 przystaje do △ BPO1 )
stąd w tym trójkącie mamy: IAO1 I2 = (1+3R)2 + R2 .........(β)
ponieważ wyrażenie (α) = wyrażenie (β)
mamy: (3−R)2 + (3R)2 = (1+3R)2 + R2
(3−R)2 − R2 = (1+3R)2 + (3R)2
(3−R+R)(3−R−R)= (1+3R+3R)(1+3R−3R)
3(3−2R)= 1+6R
9−6R = 1+ 6R
12R = 8
R= 2/3 [cm]
23 mar 17:21
komentator OWMH:
sorry
poprawy wierszy 6 powinno być:
2.− Niech środek okregu z prawej strony nazywamy O2; oraz T oznacza punkt styczności
23 mar 17:23
 |AC| = 3
|BC| = 4
Oblicz R
Ten trójkąt jest prostokątny, a okręgi takie same.
|AC| = 3
|BC| = 4
Oblicz R
Ten trójkąt jest prostokątny, a okręgi takie same.
