prosze o rozwiązanie krok po kroku.
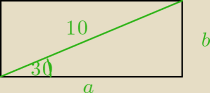
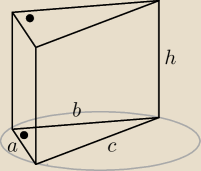
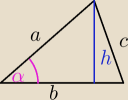
magnum2020: zad1. oblicz pole powierzchni całkowitej i objętość graniastosłup prawidłowego trójkątnego o
krawędzi podstawy mającej długość 5cm i wysokości 2 cm.
zad2. Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny o
przyprostokątnych długości: 3 √2. Suma długości wszystkich krawędzi graniastosłupa jest
równa 18( √2 + 6)cm. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
zad3. Oblicz pole powierzchni całkowitej i objetość graniastosłupa prostego, w którym podstawa
jest rombem o przekątnych długości 12cm i 16cm, a przekątna ściany bocznej ma długość 15cm.
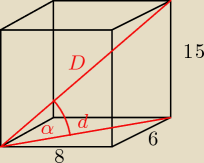
zad4. Wysokość prostopadłościanu jest równa 15cm. a krawędzie podstawy mają długość 8 i 6cm.
Oblicz tangens kąta nachylenia przekątnej prostopadłościanu do podstawy.
zad5. Przekątna ściany bocznej graniastosłupa prawidłowego czworokątnego ma długość 10 dm i
tworzy z podstawą kąt o mierze 30(stopni). Wyznacz objętość i pole powierzchni bocznej tego
graniastosłupa.
19 mar 10:57
dero2005:
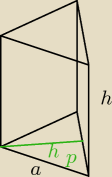
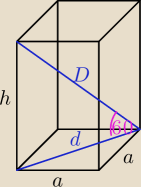
dane
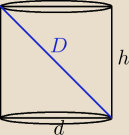
a = 5
h = 2
podstawa − trójkąt równoboczny
| | a√3 | | 5√3 | |
hp = |
| = |
| − wysokość podstawy
|
| | 2 | | 2 | |
| | a*hp | | 25√3 | |
Pp = |
| = |
| − powierzchnia podstawy
|
| | 2 | | 4 | |
| | 25 | |
Pc = 2Pp + 3*ah = |
| √3 + 30 − powierzchnia całkowita
|
| | 2 | |
| | 25√3 | |
V = Pp*h = |
| − objętość
|
| | 2 | |
19 mar 13:03
dero2005:
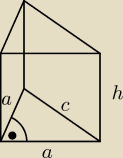
dane
a = 3
√2
L = 2(2a+c)+3h = 18(
√2+6)
c
2 = a
2+a
2 = 2a
2 = 2*18 = 36
c = 6 przeciwprostokątna
L = 4a+2c+3h
3h = L − 4a − 2c = 18
√2 + 108 − 12
√2 − 12 = 6
√2 + 96
| | 6√2 + 96 | |
h = |
| = 2√2 + 32 wysokość
|
| | 3 | |
| | a2 | |
Pp = |
| = 9 powierzchnia podstawy
|
| | 2 | |
P
c = 2*P
p + 2*ah + ch = 2*9 + 2*[3
√2(2
√2+32)] + 6*(2
√2+32) = 234 + 204
√2 pow
całkowita
V = P
p*h = 9(2
√2+32) = 18
√2 + 288 objętość
obliczenia prześledź, żeby nie było "byka"
19 mar 13:39
dero2005:
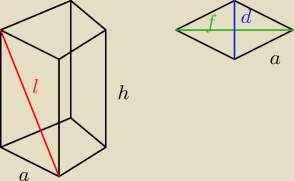
dane
f = 16 cm
d = 12 cm
l = 15 cm
tw. Pitagorasa
(
d2)
2 + (
f2)
2 = a
2
6
2 + 8
2 = a
2
100 = a
2
a = 10 cm krawędź podstawy
h =
√l2 − a2 =
√225−100 =
√125 = 5
√5 cm wysokość
P
p =
12df =
16*122 = 96 cm
2 powierzchnia podstawy
P
c = 2*P
p + 4*ah = 2*96 + 4*10*5
√5 = 192 + 200
√5 cm
2 pow całkowita
V = P
p*h = 96*5
√5 = 480
√5 cm
3 objętość
19 mar 13:56
dero2005:
d
2 = 8
2 + 6
2 = 64+36 = 100
d =
√100 = 10
19 mar 14:04
dero2005:
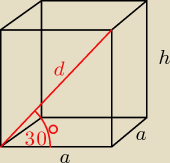
dane
d = 10 dm
a = 5
√3 dm krawędź podstawy
h = 5 dm wysokość
V = a
2*h = (5
√3)
2*5 = 375 dm
3 objętość
P
b = 4a*h = 4*5
√3*5 = 100
√3 dm
2 powierzchnia boczna
19 mar 14:13
magnum2020: w zadaniu pierwszym skad wyszlo 25√3/4? − powierzchnia podstawy
19 mar 17:12
dero2005:
| | a*hp | | 5√32 | | 25*√32 | | 25√3 | |
Pp = |
| = 5* |
| = |
| = |
| |
| | 2 | | 2 | | 2 | | 4 | |
19 mar 18:15
magnum2020: dzieki wielkie

20 mar 17:10
magnum2020: zad1. Oblicz pole powierzchni całkowitej i objętość graniastosłupa prawidłowego trójkatnego o
wysokości H=5cm i boku podstawy a=3 cm.
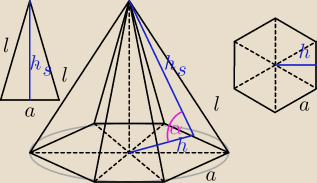
zad2. Oblicz objetość i pole powierzchni graniastoslupa prawidłowego sześciokątnego, w którym
wysokość H= 7cm, a okrąg opisany na podstawie ma promień 4cm.
zad3. Podstawą prostopadłościanu jest kwadrat. Przekątna prostopadłościanu ma długość 8√2cm i
jest nachylona do płaszczyzny podstawy pod kątem 60(stopni). Oblicz objętość i pole
powierzchni całkowitej tego prostopadłościanu.
zad4. Do akwarium z wodą wpadła metalowa kostka sześcienna o krawędzi długości 2cm. O ile
milimetrów podniósł się poziom wody, jeżeli podstawą akwarium jest prostokąt o wymiarach 10cm
x 20cm.
zad5. Podstawą graniastosłupa prostego jest romb o kącie ostrym alfa = 60(stopni). Dłuższa
przekątna graniastosłupa o długości 4dm tworzy z płaszczyzną podstawy kąt 30(stopni). Oblicz
objetość i pole powierzchni całkowitej tego graniastosłupa.
zad6. Podstawa graniastosłupa jest trójkątem prostokątnym, w którym przeciwprostokątna ma
długość 8cm , a jeden z kątów ostrych 30(stopni). Powierzchnia boczna tego graniastosłupa po
rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni o objętość graniastosłupa.
A moglbys jeszcze na te zadanka spojrzec?

20 mar 18:36
dero2005:
1)
| | a2√3 | | 9 | |
Pp = |
| = |
| √3 cm2 pole podstawy
|
| | 4 | | 4 | |
| | 9 | | 45 | |
V = Pp*h = |
| √3*5 = |
| √3 cm3 objętość
|
| | 4 | | 4 | |
| | 45 | | 9 | |
Pc = 2*Pp + 3*ah = 2* |
| √3 + 3*3*5 = |
| √3 + 45 cm2 pole całkowite |
| | 4 | | 2 | |
20 mar 19:41
dero2005:
2)
| | 3a2√3 | | 3*42√3 | |
Pp = |
| = |
| = 24√3 cm 2 pole podstawy
|
| | 2 | | 2 | |
V = P
p*h = 24
√3 *7 = 168
√3 cm
3 objętość
P
c = 2*P
p + 6*a*h = 2*24
√3 + 6*4*7 = 48
√3 + 168 cm
2 pow całkowita
20 mar 19:48
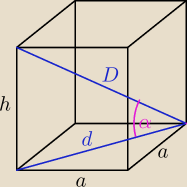
dero2005:
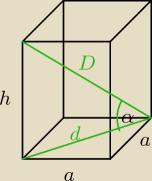
3)
D = 8
√2
α = 60
o
dD = cos α = cos 60
o =
12
h =
√D2 − d2 = 4
√6
V = a
2*h = 4*4*4
√6 = 64
√6 cm
3 objętość
P
c = 2a
2 + 4a*h = 2*4*4 + 4*4*4
√6 = 32 + 64
√6 cm
2 pow całkowita
20 mar 20:10
dero2005:
zad 4)
V = a
3 = 2
3 = 8 cm
3 objętość kostki
| | V | |
h = |
| = 810*20 = 0,04 cm = 0,4 mm |
| | 10*20 | |
20 mar 20:13
dero2005:

D = 4 dm
α = 60
o
d = D*
√32 = 4*
√32 = 2
√3
| d2 | | √3 | |
| = cos 30o = |
| rys podstawy po prawej stronie
|
| a | | 2 | |
| | d√3 | | 2√3*√3 | |
a = |
| = |
| = 2 dm
|
| | 3 | | 3 | |
| | √3 | |
Pp = a2*sin = 22*sin260o = 4*( |
| )2 = 3 dm2 pole podstawy
|
| | 2 | |
h =
√D2 − d2 =
√42 − (2√3)2 = 2 dm wysokość
V = P
p*h = 3*2 = 6 dm
3 objętość
P
c = 2*P
p + 4*a*h = 2*3 + 4*2*2 = 6 + 16 = 22 dm
2 pow całkowita
20 mar 20:40
dero2005:
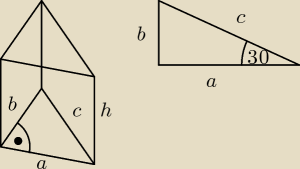
zad 5)
a = 8 cm
c = 2a = 2*8 = 16 cm
b =
√c2 − a2 =
√162 − 82 =
√256 − 64 =
√192 = 8
√3 cm
O = a + b + c = 8 + 16 + 8
√3 = 24 + 8
√3 cm
h = O wysokość
| | a*b | |
Pp = |
| = 8*8√3}{2} = 32√3 cm2 pole podstawy
|
| | 2 | |
V = P
p*h = 32
√3(24 + 8
√3) = 768(
√3 + 1) cm
3 objętość
P
c = 2*P
p + O
2 = 2*32
√3 + (24 + 8
√3)
2 = 64
√3 + 768 + 384
√3 = 448
√3 + 768 cm
2
powierzchnia calkowita
20 mar 21:07
dero2005:
w zadaniu o rombie wkradł się błąd:
wiersz czwarty od końca powinno być
| | √3 | |
Pp = a2*sin α = 22* sin 60o = 4* |
| = 2√3 dm2
|
| | 2 | |
h = bez zmian
V = P
p*h = 2
√3*2 = 4
√3 dm
3
P
c = 2*P
p + 4*ah = 2*2
√3 + 4* 2*2 = 4
√3 + 16 dm
2

21 mar 07:27
magnum2020: dzieki

21 mar 16:59
magnum2020: a mozesz mi wytlumaczyc jak sie zabrac do takiego zadania zeby je wykonac?

23 mar 16:52
dero2005:
ostrożnie

a o które zadanie chodzi?
23 mar 17:20
magnum2020: np. te 3

.
23 mar 18:26
magnum2020: a w zadaniu 1, z drugiej listy tych zadan wzór na pole pow.calkowitej nie powinien byc
Pc=2Pp+Pb? czy ten "Pc = 2*Pp + 3*ah" to jest dobrze?
23 mar 18:56
dero2005:
odpowiedź: zad 1 z drugiej serii
Pc = 2*Pp + Pb gdzie Pp − pole podstawy Pb − pole boczne Pc − pole całkowite
Zauważ, że pole boczne graniastosłupa o podstawie trójkąta równobocznego jest równe sumie pól
trzech bocznych ścian czyli Pb = a*h + a*h + a*h = 3a*h czyli to samo. Napisałem tam 3ha,
żeby urozmaicić monotonię rozwiązywania zadań, które są bardzo podobne.
23 mar 19:12
magnum2020: ok rozumiem

..czyli Pb rombu to bd, Pb=4ah? i tak z kazda figura tyle ile scian to razy tyle
mnozymy a z h?

.. a jak bym nie mial "a" lub "h" to jak je wyznaczyc?
23 mar 19:19
dero2005:
widzę że zaskoczyłeś bo to naprawdę proste. W ganiastosłupach prostych ściany są prostokątami
lub kwadratami więc liczysz pole jednej ściany i mnożysz przez ilość ścian, czyli krawędź
podstawy razy wysokość razy ilość ścian. Jeżeli nie ma podanej długosci krawędzi lub wysokości
to podane są inne dane np. przekatna sciany i kąt nachylenia przekątnej. W ostrosłupach ściany
są trójkatami więc liczysz pole trójkata w zależności od tego co jest dane i mnożysz przez
ilość ścian.

23 mar 19:40
magnum2020: a w tym zadaniu 3. w tych drugich zadanich. co oznacza male "d"? i skad sie wzial ten wzor na
"a"? i dlaczego d/D = cos? i ostanie pytanie. Jak powstal ten wzro na Pc?
23 mar 21:38
dero2005:
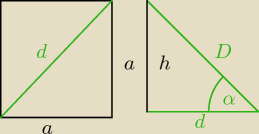
już tłumaczę
d − przekątna podstawy (kwadratu)
z Pitagorasa
a
2 + a
2 = d
2
2a
2 = d
2
w trójkącie prostokątnym stosunek przyprostokątnej leżacej przy kącie do przeciwprostokątnej
nazywamy cosinusem kąta α (rysunek po prawej stronie)
P
c − powierzchnia całkowita
P
c = 2 razy pole podstawy + 4 razy pole ściany
P
c =2*a
2 + 4*a*h gdzie a − krawędź podstawy h − wysokość ściany
23 mar 21:58
magnum2020: dzieki

teraz juz rozumiem. A ten wzro h = √D2 − d2 = 4√6 to jest na wysokosc rombu? i dlaczeg
ow zadaniu 3 i 5 wzory na male "d" sa rozne? i dlaczego w zadaniu 5 oczywiscie tej drugiej
listy zadań Pp − wystepuje sin?
24 mar 17:04
magnum2020: a i w zadaniu 5, dlaczego male a=d√3 przez 2..a nie √2?
24 mar 17:05
magnum2020: I jak bd mial czas to jeszcze bym prosil o wytlumaczenie zadania 2. z pierwszej listy zadan

.
Bo z tymi "L" to wgl. sie pogubilem o co tam chodzi

24 mar 17:08
dero2005:
wzór h =
√D2−d2 = 4
√6 jest to wzór na wysokość graniastosłupa prawidłowego prostego
czworokątnego, czyli o podstawie kwadratu
Przekątna kwadratu d = a
√2
przekształca się go z tw Pitagorasa , przekątna podstawy d, wysokość h, przekątna
graniastosłupa D tworzą trójkąt prostokątny
D
2 = d
2 + h
2
h
2 = D
2 − d
2
h =
√D2−d2
w zad 3 i 5 wzory na d są różne gdyż w 3 zad kąt α = 60
o a zad 5 α = 30
o a cos 60
o =
12
| | √3 | |
, cos 30o = |
| stąd różnica
|
| | 2 | |
P
p = a
*sin α − jest to wzór na pole powierzchni rombu gdy jest dane bok rombu i kąt ostry α
| d2 | | √3 | |
| = |
| mnożymy na krzyż
|
| a | | 2 | |
2*
d2 = a
√3
d = a
√3 |:
√3
| | d | |
a = |
| żeby pozbyć się niewymierności w mianowniku mnożymy licznik i mianownik
|
| | √3 | |
przez
√3
| | d | | √3 | | d√3 | | d√3 | |
a = |
| * |
| = |
| = |
|
|
| | √3 | | √3 | | √3*√3 | | 3 | |
w zad 2 jest podana długość wszystkich krawędzi i przyprostokątne trójkąta podstawy czyli
brakuje nam długości przeciwprostokątnej podstawy i wysokości h
przeciwprostokątną można policzyć z tw. Pitagorasa
c
2 = 2a
2
c = a
√2
wtedy sumujemy wszystkie krawędzie i obliczamy h
4a + 2c + 3h = 18(
√2+6)
z tego wzoru obliczamy h
3h = 18(
√2+6) − 2c − 4a
24 mar 20:38
magnum2020: Dzieki teraz juz rozumiem

. A mogłbys jeszcze na te zadanka spojrzeć? i pokazać mi jak to się
je rozwiązuje krok po kroku?

zad1. Wysokość ostrosłupa prawidłowego jest równa 3, a jego podstawą jest kwadrat o boku 4
√2.
Narysuj siatkę tego ostroslupa i oblicz jesgo pole powierzchni calkowitej.
zad2. Podstawą ostrosłupa jest kwadrat ABCD o boku długosći 6. Ściana boczna ABS jest
prostopadła do podstawy oraz |AS|=|BS|=5. Narysuj siatkę tego ostrosłupa i oblicz jego pole
powierzchni calkowitej.
zad3. Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe polu jego podstawy.
Oblicz sinus kąta naychlenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
zad4. Wysokosć ostrosłupa prawidłowego trójkątnego jest równa
√3, a kąt nachylenia ściany
bocznej do płaszczyzny podstawy ma miarę 30(stopni). Oblicz objętość i pole powierzchni
bocznej tego ostrosłupa.
zad5. Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny
podstawy pod kątem 30(stopni), a jej wysokość jest równa 3
√3. Oblicz objętość tego
ostrosłupa.
zad6. Podstawą ostroslupa o wierzchołku S jest trójkąt ABC o bokach długości: |AB|=6, |AC|=
|BC|= 5. Wysokość ostrosłupa jest równa 2, a jej spodek jest środkiem okręgu opisanego na
podstawie. Oblicz tangens kąta nachylenia ściany ABS do płaszczyzny podstawy ostrosłupa.
zad7. Ostrosłupa prawidłowy czworokątny, którego krawędź boczna ma długość 5, a przekątna
podstawy 8, przecieto płaszczyznę równoległą do podstawy, przechodzącą przez środek jesgo
wysokości. Oblicz bojętość części, na które ta płaszczyzna podzieliła ostrosłup.
26 mar 14:12
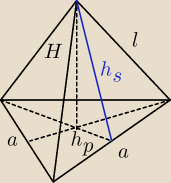
dero2005:
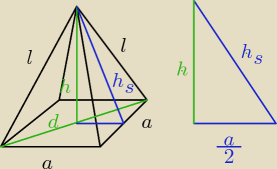
zad1)
dane:
a = 4
√2 − krawędź podstawy
h = 3 − wysokość ostrosłupa
oznaczenia:
d − przekątna podstawy (kwadratu)
h
s − wysokość ściany bocznej (trójkąta)
l − krawędź boczna (ramię trójkąta równoramiennego o podstawie a)
Z trójkąta prostokątnego liczymy h
s wg tw. Pitagorasa
h
s2 = (
a2)
2 + h
2 = (
4√22)
2 + 3
2 = (2
√2)
2 + 9 = 8 + 9 = 17
h
s =
√17
P
p − pole podstawy (pole kwadratu)
P
p = a
2 = (4
√2)
2 = 32
P
s − pole ściany bocznej (pole trójkąta)
| | a*hs | | 4√2*√17 | |
Ps = |
| = |
| = 2√34
|
| | 2 | | 2 | |
P
b − pole powierzchni bocznej (czterech ścian−trójkątów)
P
b = 4*P
s = 4*2
√34 = 8
√34
P
c − pole całkowite
P
c = P
b + P
p = 32 + 8
√34 = 8(4 +
√34)
liczymy l dla rysowania siatki
l
2 = (
a2)
2 + h
s2 = (2
√2)
2 + (
√17)
2 = 8 + 17 = 25
l =
√25 = 5
26 mar 15:41
dero2005:
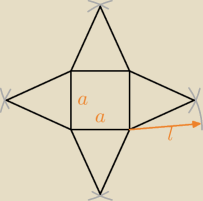
siatka ostrosłupa do zad 1
26 mar 16:10
dero2005:
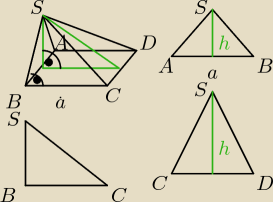
zad 2)
dane:
a = |AB| = |BC| = |CD| = |AD|
a = 6
|BS| = |AS| = 5
liczymy wysokość trójkąta ABS
h =
√|AS|2 − (a2)2 =
√52 − 32 =
√25−9 =
√16 = 4
liczymy powierzchnię trójkąta ABS
| | a*h | | 6*4 | |
PABS = |
| = |
| = 12
|
| | 2 | | 2 | |
rozpatrujemy bok BCS (takich boków jest dwa)
|BC| = a = 6
|BS| = 5
pole powierzchni
| | |BC|*|BS| | | 5*6 | |
PBCS = |
| = |
| = 15
|
| | 2 | | 2 | |
liczymy długość boku |CS|
|CS|
2 = |BC|
2 + |BS|
2 = 6
2 + 5
2 = 36 + 25 = 61
|CS| =
√61
rozpatrujemy bok CDS
wysokość h (z Pitagorasa)
h =
√|CS|2 − (|CD|2)2 =
√(√61)2 − 32 =
√61−9 =
√52 = 2
√13
pole powierzchni
| | |CD|*h | | 6*2√13 | |
PCDS = |
| = |
| = 6√13
|
| | 2 | | 2 | |
liczymy pole powierzchni całkowitej, na które składa się pole podstawy + pole boku ABS +
+ 2*pole boku BCS + pole boku CDS
P
c = a
2 + P
ABS + 2* P
BCS + P
CDS
P
c = 6
2 + 12 + 2*15 + 6
√13 = 36 + 12 + 30 + 6
√13 = 78 + 6
√13 = 6(13 +
√13)
26 mar 17:13
dero2005:
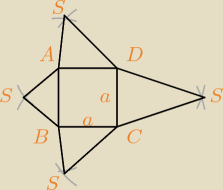
siatka do zad 2)
rysujemy kwadrat o boku a, następnie cyrklem z punktu A i B zakreślamy długości |BS|=|AS|,
z punktów C i D zakreślamy odcinki |CS| = |DS|. W ten sposób znajdujemy punty S
Na rysunku nie jest to proporcjonalne bo nie miałem cyrkla, jest to tylko rysunek poglądowy
26 mar 17:29
dero2005:
zad 3)
rys jak do zad 1
h
s = 2a
h =
√hs2 − (a2)2 =
√4a2 − a24 =
a2√15
26 mar 20:36
dero2005:
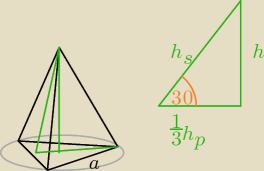
Zad4)
dane:
h =
√3
α = 30
o
oznaczenia
h
s − wysokość ściany bocznej
h
p − wysokość podstawy
a − krawędź podstawy
h
s = 2h = 2
√3
h
p =
23h
s√3 = 4
| | a*hs | |
Pb = 3* |
| = 24 pow boczna
|
| | 2 | |
| | a2√3 | | 16 | |
Pp = |
| = |
| √3 pow podstawy
|
| | 4 | | 3 | |
| | 16 | |
V = 13Pp*h = 13*16*√33*√3 = |
| objętość
|
| | 3 | |
27 mar 12:33
dero2005:
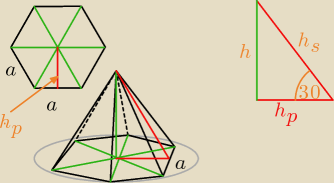
Zad 5)
dane
h
s = 3
√3 wysokość ściany bocznej
α = 30
o nachylenie ściany
oznaczenia
a − krawędź podstawy
h − wysokość ostrosłupa
h
p − odległość spodka wysokości od krawędzi
| | 3a2√3 | | 81√3 | |
Pp = |
| = |
| pole podstawy
|
| | 2 | | 2 | |
| | 243 | |
V = 13*Pp*h = |
| objętość
|
| | 4 | |
27 mar 13:07
dero2005:
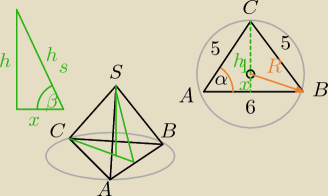
zad 6)
dane
|AB| = 6
|AC| = 5
|BC| = 5
h = 2
h
1 =
√52 − 32 =
√25−9 =
√16 = 4 wysokość podstawy
| | h | | 2 | | 16 | |
tg β = |
| = |
| = |
| = 227
|
| | x | | 78 | | 7 | |
27 mar 15:58
magnum2020: moglbys jeszcze jedno te zadanie zrobic?

. z gory dzieki

28 mar 15:39
magnum2020: moglbys jeszcze jedno te zadanie zrobic?

. z gory dzieki

28 mar 15:39
magnum2020: moglbys jeszcze jedno te zadanie zrobic?

. z gory dzieki

28 mar 15:39
xx: dero chciało ci się to pisać wszystko? rysunki chyba z 6h robileś
28 mar 17:40
dero2005:
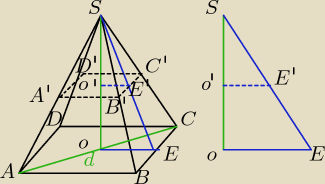
dane
|AC| = d = 8 − przekątna podstawy
|CS| = l = 5 − krawędź boczna
liczymy a − krawędź podstawy
2a
2 = d
2a
2 = 8
a
2 = 4
a = 2
liczymy h − wysokość ostrosłupa |OS| z trójkąta OCS
h =
√l2 − (d2)2 =
√52 − 42 =
√25−16 =
√9 = 3
liczymy objętość ostrosłupa ABCDS
V =
13a
2*h =
13*2
2*3 = 4
liczymy |O'E'| z podobieństwa trójkątów OES i O'E'S
gdzie:
|SO| = h = 3
|OE| =
a2 = 1
|SO'| =
h2 =
32
| | |SO'|*|OE| | |
|O'E'| = |
| = 12
|
| | |SO| | |
liczymy objętość ostrosłupa A'B'C'D'S
|A'B'| = 2*|O'E'| = 2*
12 = 1 = a
1 krawędź podstawy "mniejszej"
|SO'| =
32 = h
1 wysokość ostrosłupa "mniejszego"
V
1 =
13*a
12*h
1 =
13*1
2*
32 =
12
liczymy objętość ostrosłupa ABCDA'B'C'D'
V − V
1 = 4 −
12 = 3
12
odpowiedź: objętość części wynoszą odpowiednio 3
12 i
12
28 mar 18:38
magnum2020: dzieki bardzo

. za pomoc

29 mar 14:47
magnum2020: Jeszcze bys mogl zerknac na te zadanka?

zad1. Dany jest prostokat mający boki 4cm i 8cm. Środki boków prostokąta są wierzchołkami
rombu. Wyznacz pole tego rombu.
zad2. Wysokość trójkąta równobocznego wynosi 2
√3. Wyznacz jego obwód.
zad3. Liczby 8,15,x są długościami boków trójkąta prostokątnego. wyznacz x.
zad4. Podstawy trapezu równoramiennego mają długość 10cm i 12cm a ramię ma długość 4cm. Oblicz
pole tego trapezu.
zad5. Przekątna kwadratu jest równa P{5}. Oblicz obwód tego kwadratu.
zad6. Dłuższa przyprostokątna trójkąta prostokątnego ma długość 9, a jeden z kątów ostrych
30(stopni). Wyznacz pole tego trójkąta.
29 mar 14:56
dero2005:
zad1)
P =
12a*b =
124*8 = 16
zad2)
O = 3a = 12
zad3)
x
2 = 15
2 + 8
2
x
2 = 289
x =
√289 = 17
zad4)
h =
√42 − (12−102)2 =
√15
zad5)
| | d√2 | | √5*√2 | | √10 | |
a = |
| = |
| = |
|
|
| | 2 | | 2 | | 2 | |
O = 4a = 2
√10
zad6)
b = 3
√3
29 mar 19:57
- Master -: Widze ze "dero2005" jeste dobry w te klocki ! Gratuluje takich zdolnosci matematycznych

29 mar 20:04
magnum2020: dzieki

, a mozesz jeszcze te zrobic? bo chce sprawdzic czy dobrze je sam rozwiazalem

.
zad1. Wyznacz miarę kąta ostrego rombu którego pole jest rowne 24
√3 a jego wysokosc 6.
zad2. Wyznacz promień okręgu wpisanego w trójkat równoboczny o boku 6.
zad3. Przekątna prostokata o długości 10cm tworzy z dłuższym bokiem kąt 30(stopni). Wyznacz
pole tego prostokąta.
zad4. Obwód trójkąta równobocznego jest równy 32cm. Podstawa tego trójkąta jest o 1 cm dłuższa
od ramienia. Wyznacz długość ramienia tego trójkąta.
zad5. Oblicz pole równoległoboku o bokach długości 1 dm i 4cm oraz kącie rozwartym o mierze
140(stopni).
zad6. Wyznacz równanie okręgu o środku S (−1,3) i promieniu 4.
30 mar 15:57
dero2005:
napisz rozwiązania to powiem czy dobrze

30 mar 19:05
magnum2020: Kurde kolega mi to sprawdzal i same glupoty mi powychodzily

. Jak nie mozesz ich rozwiazac to
ok, pojde do kolegi zeby mi w tym pomogl

30 mar 20:27
dero2005:
zad 1)
P = a*h = 24
√3
P = a
2sinα
| | P | | 24√3 | | √3 | |
sinα = |
| = |
| = |
|
|
| | a2 | | (4√3)2 | | 2 | |
α = 60
o
Zad2)
r =
13h
r =
13*
6*√32 =
√3
Zad3)
rysunek do zad 3
a = 5
√3
b =
√102 − (5√3)2 =
√25 = 5
P= a*b = 5*5
√3 = 25
√3
30 mar 20:45
dero2005:
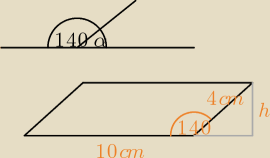
zad5)
α = 180 − 140 = 40
o
h4 = sin 40
o = 0,6427
h = 4* 0,6427 = 2,57 cm
P = a*h = 10 * 2,57 = 25,7 cm
2
30 mar 20:53
dero2005:
zad 6)
(x−xo)2 + (y−yo)2 = r2 równanie okręgu
S = (xo,yo) = (−1, 3) r = 4
(x + 1)2 + (y − 3)2 = 16
30 mar 20:56
dero2005:
w zadaniu 4 nie wiadomo czy jest trojkąt równoboczny czy równoramienny. Zdecyduj się

30 mar 20:57
magnum2020: równoboczny

. taka tresc zadania w szkole dostalem: "Obwód trójkąta równobocznego jest równy
32cm. Podstawa tego trójkąta jest o 1 cm dłuższa
od ramienia. Wyznacz długość ramienia tego trójkąta."
30 mar 21:04
dero2005:
jeżeli jest równoboczny to dlaczego podstawa jest dłuższa od ramienia

30 mar 21:40
dero2005:
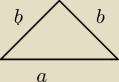
przyjmuję wstępnie ,że jest to trójkąt równoramienny
2b + b + 1 = 32
3b = 32 − 1
3b = 31
b =
313
30 mar 21:44
magnum2020: tak, jest to rownoramienny, zle doczytalem

. dzioeki

31 mar 13:46
magnum2020: w zadaniu 2 z tych pierwszych zadan z planimetri. skad sie wzial ten wzor na "a" tam gdzie a=4.
31 mar 13:53
magnum2020: i w tym zadaniu 5 z tej pierwszej listy skad wzial sie wzor na a?
31 mar 13:59
dero2005:
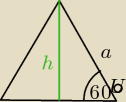
31 mar 17:09
dero2005:
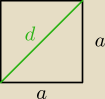
tw Pitagorasa
a
2 + a
2 = d
2
2a
2 = d
2
a
2 =
d22
| | √d2 | | d | | √2 | | d√2 | |
a = |
| = |
| * |
| = |
| |
| | √2 | | √2 | | √2 | | 2 | |
31 mar 17:15
magnum2020: dzieki

A moglbys jeszcze na to zerknać? powinno wyjsc 288cm
3. ale nie wychodzi cos

zad. Oblicz objetość ostrosłupa prawidłowego trójkątnego, w którym wysokość jest równa 24 a
wysokość
ściany bocznej wynosi 26.
4 kwi 20:42
morfepl: a już liczyłem na jakiś offtop

4 kwi 20:43
magnum2020: mozesz mi przeslac link bo nei moge znalesc?
4 kwi 20:50
pomagacz:
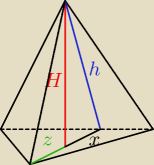
H = 24
h = 26
1.
długość krawędzi podstawy:
wyprowadzasz a, obliczasz.
2.
z prawa pitagorasa:
H
2 + x
2 = h
2
x
2 = h
2 − H
2
x =
√h2 − H2
x =
√262 − 242
x =
√676 + 576
x =
√100
x = 10
gdzie x =
13z (wysokości podstawy)
pole podstawy:
4 kwi 21:07
;)))))): NIezla lektura

4 kwi 21:09
morfepl: oczywiście wyższa inteligencja musiała splugawić to kompendium wiedzy z plani/stereo−metrii
4 kwi 21:16
-Fifty-:
CZesc.
Czy potrafil by mi ktos rozwiazac te zadanka, bo jutro z tego musze zaliczyc semestr...
rysunek jest do zadania 5.
zad.1
Oblicz objetosc i pole powierzchni calkowitej czworoscianu foremnego ktorego krawedz ma dlugosc
6
√2
zad.2
Onlicz objetosc ostrosłupa prawidłowego trójkatnego, w ktorym wysokosc jest rowna 24, a
wysokosc sciany bocznej wynosi 26
zad.3
Oblicz pole powierzchni i objetosc ostrosłupa prawidłowego czworokatnego, ktorego krawedz
podstawy ma długosc 5 a krawedz boczna 8.
zad.4
Podstawa ostrosłupa jest trójkat prostokatny o przyprostokatnych 16 i 12. Kazda krawedz boczna
ostrosłupa jest nachylona do płaszczyzny podstawy po katem 60stopni. Oblicz objetosc
ostrosłupa.
zad.5
rys:(tam gdzie jest czerwona kropka na dole jest 12, a tam gdzie jest kropka z boku jest 14)
Wyznacz objetosc i pole powierzchni calkowitej ostroslupa prawidlowego trojkatnego.
5 kwi 15:21
Bartek: to nic nie znaczy
9 maj 21:25
justa: pole podstawy graniastosłupa czworokątnego jest równe 16cm2 .Oblicz objętość tego
graniastosłupa jeśli przekatna ma długość 9 cm
17 wrz 17:17
dero2005:
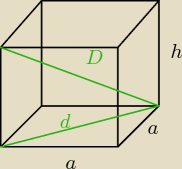
czy to jest graniastosłup prawidłowy? tzn czy podstawa jest kwadratem? Zakładam , że tak.
D = 9 cm
P
p = a
2 = 16 cm
2
a =
√16 = 4 cm
d = a
√2 = 4
√2 cm
h =
√D2 − d2 =
√81 − 32 =
√49 = 7 cm
V = P
p*h = 16*7 = 112 cm
3
17 wrz 21:15
beatakochut: narysuj siatkę ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 3cm i wysokości sciany
bocznej równej 2cm.oblicz pole powierzchni całkowitej ostrosłupa?
3 maj 10:34
dzaniel707:
oblicz pole siatki ostros8,5cm i 10cmupa
4 cze 19:54
d.: w rombie o długości boku a=6 kat ostry ma miare l=45 oblicz pole i obwód rombu
6 cze 21:07
Dominika: Oblicz pole całkowite graniastosłupa prawidłowego sześciokątnego, jeżeli dłuższa przekatna
graniastisłupa jest nachylona do podstawy pod kątem 60stopni, a wysokość tego graniastisłupa
wynosi 4 pierwiastki z 3 cm.
19 sie 14:44
dero2005:
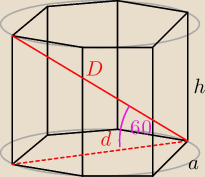
h = 4
√3
a = 2
P
b = 6a*h =
P
c = 2P
p + P
b =
19 sie 17:05
Iga: 1. Oblicz objętość i pole całkowite graniastosłupa prawidłowego trójkatnego, jeżeli przekątna
ściany bocznej tworzy z krawędzią boczną kąt 45stopni.
2.Oblicz objętość i pole całkowite sześciokąta foremnego, gdy dłuższa przekątna graniastosłupa
o długości 9 tworzy z krótszą przekatną podstawy kąt o mierze 60stopni.
22 sie 18:57
Iga:
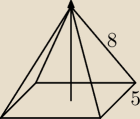
Oblicz objętość
22 sie 19:01
dero2005:
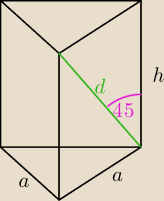
zad 1
a = h
P
b = 3a*h = 3a
2
P
c = 2P
p + P
b = a
2(
√32+3)
22 sie 23:00
dero2005: zad 2
sześciokąt nie ma objętości bo to jest figura płaska
22 sie 23:01
dero2005:
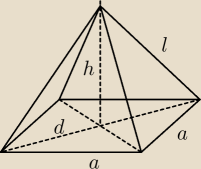
a = 5
l = 8
d = a
√2 = 5
√2
| | √206 | |
h = √l2 − (d2)2 = √64 − 252 = |
| |
| | 2 | |
P
p = a
2 = 25
22 sie 23:11
dero2005:
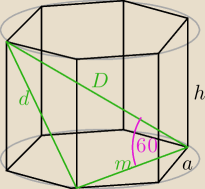
D = 9
m = a
√3
| | 9√15 | |
d = √D2 − m2 = √81 − 8116 = |
| |
| | 4 | |
P
b = 6a*h =
P
c = 2*P
p + P
b =
V = P
p*h =
policz wyniki bo mogą być błędy
22 sie 23:30
Dorota: oblicz objętośc graniastosłupa prawidłowego czworokątnego, którego wysokośc ma 16cm , a krawędz
podstawy jest 4 razy krótsza
10 wrz 15:27
Sandra;#62;: Cześć. Czy dostalabym rozwiązanie na te dwa zadanka?;x . Zalezy mi bardzo, gdyż próbuję się
przygotowywać do matury, a sama sobie nie poradzę.
Zad1 Oblicz pole i obwód trapezu równoramiennego
opisanego na okręgu o promieniu 4 cm, jesli jedna z podstaw jest o 12 cm dłuższa od drugiej.
Zad 2. W
trapez równoramienny o kącie 45 stopni wpisano okrąg o promieniu 1 cm. Oblicz długości podstaw
tego trapezu. Z góry Dziękuję;>
18 wrz 18:13
dero2005:
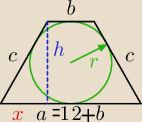
h = 2r = 8
c =
√x2 + h2 =
√36+64 = 10
2c = 12+b+b
c= 6+b
b = 10−6 = 4
a = 12+b = 16
| | a+b | | 16+4 | |
P = |
| *h = |
| *8 = 80 |
| | 2 | | 2 | |
O = 2c+a+b = 10+16+4 = 30
18 wrz 20:31
dero2005:
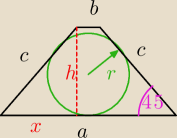
r = 1
h = 2r = 2
x = h = 2
c =
√x2+h2 = 2
√2
b = 2(
√2−1)
a = 2(
√2+1)
18 wrz 20:44
joanna4: oblicz długosc okregu opisanego na trojkacie prostokatnym jesli wiadomo ze długosc jednej
przyprostokatnej trojkata jest rowna 6 dm i przyprostokatna ta tworzy z przeciwprostokatna kat
o mierze 30 stopni
3 paź 17:34
dero2005:
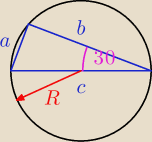
b = 6 dm
O = 2πR = 4π
√3
3 paź 17:59
wiktoria3: oblicz długosc okregu opisanego na trójkacie prostokatnym jesli wiadomo ze długosc jednej
przyprostokatnej tego trojkata wynosi 16 cm i przyprostokatna ta tworzy z przeciwprostokatna
kat o mierze 40 stopni
3 paź 20:31
dero2005:
j.w
3 paź 20:40
wiktoria3: w okrąg o promieniu 10 dm wpisano trójkąt rownoramienny którego podstawa ma długość 16 dm
oblicz długosc ramion trojkata rozwiaz dwa przypadki
3 paź 22:35
wiktoria3: wysokosc CD w trojkacie równobocznym ABC o boku długosci 12 cm dzieli ten trojkat na dwa
trojkaty prostokatne oblicz stosunek długosci promienia okregu opisanego na trojkacie
rownobocznym ABC do długosci promienia okregu opisanego na trojkacie prostokatnym BCD
3 paź 22:39
dero2005:
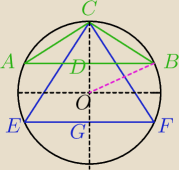
OB = OC = 10
BD = GF = 8
DO =
√102−82 = 6
DC = OC − OD = 10−6 = 4
CB =
√DB2 + DC2 =
√82 + 42 =
√80 = 4
√5
GO = DO = 6
GC = GO + OC = 6 + 10 = 16
FC =
√GF2 + GC2 =
√82 + 162 =
√320 = 8
√5
3 paź 23:00
dero2005:
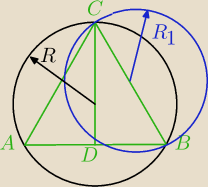
AB = BC = CD = a = 12
R =
23h = 4
√3
3 paź 23:13
wiktoria3: Dla jakich wartości a punkty A, B, C takie, że |AB|=a+3, |BC|=2a−5, |AC|=4−3a, są wierzchołkami
trójkąta?
5 paź 12:22
wiktoria3: Uzupełnij zdanie tak, aby było prawdziwe.
Wpisz w każdą lukę odpowiednią liczbę.
Stosunek długości przyprostokątnych trójkąta prostokątnego o obwodzie 60 cm wynosi 5:12.
Krótsza przyprostokątna tego trójkąta ma długość_____cm, a dłuższa – ____ cm.
5 paź 12:25
wiktoria3: Połącz rodzaj trójkąta z przykładowymi długościami jego boków.
Przy każdym numerze wpisz odpowiednią literę.
I. trójkąt ostrokątny II. trójkąt prostokątny III. trójkąt rozwartokątny
A. 2√3 √5, 3√2 B. 2√7, √5, 2√6 C. 3√,3 2√5, √7
I – II – III –
5 paź 12:28
wiktoria3: Uzupełnij zdanie tak, aby było prawdziwe.
Wpisz w każdą lukę odpowiednią liczbę.
Minimalny promień garnka, do którego można wstawić cztery słoiki o średnicy 10 cm, to (__ +
__√2) cm.
5 paź 12:34
niewana21: Proszę o pomoc z tym zadaniem..
Podstawą ostrosłupa jest romb o kącie ostrym 30 stopni i boku długości 2 cm. Objętość jest
równa:
| | 2 | |
A. |
| długości krawędzi podstawy |
| | 3 | |
| | 3 | |
B. |
| długości krawędzi podstawy |
| | 2 | |
C. o 7 dłuższa od krawędzi podstawy
D. o 7 krótsza od krawędzi podstawy.
7 paź 21:15
anka: graniastosłup prawidłowy czworokątny wysokość jest 5 razy dłuższa od krawędzi podstawy. dane
jest pole powierzchni całkowitej np.500. Oblicz objętość
24 paź 18:48
dero2005:
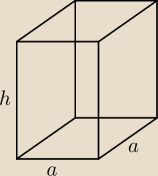
h = 5a
P
c = 2a
2 + 4ah = 500
2a
2 + 4*a*5a = 500
22a
2 = 500
V = a
2*h = a
2*5a = 5a
3 = 5*(
√50022)
3
24 paź 20:12
nik: Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny , którego
przeciwprostokątna ma taką samą długość jak wysokość graniastosłupa. Oblicz objętość i pole
powierzchni całkowitej tego graniastosłupa, wiedząc, że obwód podstawy jest równy (12 + 6√2)
cm .
5 lis 18:41
dero2005:
c = h
a = b
2a + c = 12 + 6
√2
2a
2 = c
2
rozwiąż układ równań, policzyć a, b=a , c = h
P
b =(2a+c)*h
P
c = 2*P
p + P
b
V = P
p*h
5 lis 21:18
Dominik: W ostrosłupie prawidłowym trojkątnym , wysokość podstawy ma długość 6 cm . Kąt nachylenia
krawędzi bocznej do płaszczyzny podstawy ma miarę 30 stopni . Oblicz V i Pc.
11 lis 09:01
dero2005:
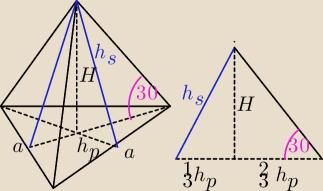
h
p = 6 cm
h
s2 = (
13h
p)
2 + H
2
P
c = P
p +P
b = 12(
√3 +
√7) cm
2
11 lis 09:23
buda13sk: oblicz objentość i pole całkowite sześcianu o krawędzi długość 5cm
14 lis 16:24
buda13sk: oblicz objentość i pole całkowite sześcianu o krawędzi długość 5cm
14 lis 16:24
buda13sk:
14 lis 16:25
mephiu: V = a3 = 53 = 125 cm3
Pc = 6a2 = 6*52 = 6*25= 150cm3
14 lis 16:27
dero2005:
V = a3 = 53 = 125
Pc = 6a2 = 6+52 = 150
14 lis 16:59
hyhy;): 2+8=
18 lis 17:11
buda13sk: rozwiązecie mi zadanie? Podstawa graniastosłupa wynosi 42cm kwadratowych a jego wsokość 9cm.
Oblicz objętość tego graniastosłupa. Pomożecie
18 lis 17:13
wiola: W graniastosłupie prawidłowym czworokątnym przekątna o długosci24cm tworzy z płaszczyzną
podstawy kąt 60*.Oblicz pole powierzchni całkowitej tego graniastosłupa.
proszęo zerkniecie

19 lis 17:48
wiola: jeszcze to plisss
zad1.
Oblicz pole całkowite i objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy
równej 10 cm wiedząc że jego wysokosć jest o 20% dłuższa od krawędzi podstawy.(rys)
zad 2.
Oblicz pole powierzchni całkowitej walca którego promień podstawy wynosi 8 cm i jest 2 razy
krótszy od wysokości walca.Ile wynosi objętość tego walca?
zad 3.
19 lis 17:54
dero2005:
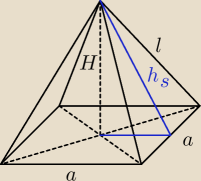
zad1
a = 10
H = 1,2a = 12
h
s =
√H2 + (a2)2 =
√122 + 52 =
√169 = 13
P
p = a
2 + 2a*h
s =
19 lis 19:10
dero2005:
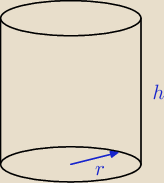
r = 8
h = 2r = 16
P
c = 2πr(r + h) =
V = πr
2*h =
19 lis 19:18
Misia201: Wie ktoś może jak rozwiązać logarytm..:
19 lis 19:21
Misia201: ... proszę pomocy ..

na serio tego nie ogarniam
19 lis 19:22
dero2005:
D = 24
d = 12
h =
√D2 − d2 =
√242 − 122 =
√432 = 12
√3
P
c = 2a
2 + 4ah =
19 lis 19:34
dero2005:
| | √18 | |
12log4 18 − log4 24 = log4 √18 − log4 24 = log4 |
| = |
| | 24 | |
| | 212 | |
22x = |
| = 212−3 = 2−52 |
| | 23 | |
x = −
54
19 lis 19:44
Marysia: 1.Krawędź podstawy graniastosłupa prawidłowego trójkątnego ma dł 2 ,a jego pole powierzchni
całkowitej jest równe 24.Oblicz wysokość tego graniastosłupa.
20 lis 13:01
Marysia: Proszę o pomoc :
zad 1.Krawędź podstawy graniastosłupa prawidłowego trójkątnego ma dł 2 ,a jego pole powierzchni
całkowitej jest równe 24.Oblicz wysokość tego graniastosłupa.
zad 2 Przekątna graniastosłupa prawidłowego czworokątnego ma dł 8 i jest nachylona pod kątem
którego cosinus wynosi jedna czwarta.Oblicz objętość tego graniastosłupa.
Zad 3 Oblicz pole powierzchni całkowitej i objętość sześcianu,którego przekątna jest o 2
dłuższa od jego krawędzi.
20 lis 13:09
dero2005:
zad1
a = 2
| | a2√3 | | 3 | |
Pc = |
| + |
| a*hs = 24 |
| | 4 | | 2 | |
H =
√hs2 − (13hp)2 =
√192−16√33
20 lis 17:27
dero2005:
zad 2 " i jest nachylona ( do czego ?) pod kątem"
D = 8
h =
√D2 − d2 =
√64 − 4 =
√60 = 2
√15
V = a
2*h = 4
√15
20 lis 17:33
dero2005:
zad3
D = a
√3
D = a + 2
a
√3 = a + 2
a
√3 − a = 2
a(
√3−1}) = 2
P = 6a
2 = 12(
√3+2)
V = a
3 = 2(3
√3 + 5)
20 lis 17:42
Marysia: jest nachylona do podstawy
20 lis 17:44
piotr: x−3+x≤3
20 lis 17:47
Marysia: O ja Cię już bardzo bardzo lubię −jestem winna Ci chyba dobrą kawę.
zad 4
podstawy trapezu równomiernego mają dł 2 cm i 6 cm,a cosinus kąta przy dłuższej podstawie jest
równy jedna trzecia.Oblicz obwód trapezu.
zad 5
Dwa boki trójkąta mają długości 3√3 i 6, a kąt między nimi zwarty na miarę 30 stopni.Oblicz
pole tego trójkąta
20 lis 17:49
dero2005:
x−3+x≤3
2x≤6
x≤3
20 lis 17:51
dero2005:
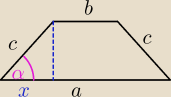
zad 4
a = 6
b = 2
c = 3x = 6
O = a + b + 2c = 20
20 lis 17:57
dero2005:
a = 3
√3
b = 6
α = 30
o
20 lis 18:12
Marysia: Zad.6 Prostokąt o polu 12 cm kwadratowych ma obwód równy 14 cm.Podaj wymiary
tego prostokąta
20 lis 18:19
dero2005:
a
1 = 4 b
1 = 3
a
2 = 3 b
2 = 4
20 lis 18:25
Kinga: 1.Dany jest ostrosłup prawidłowy czworokątny. Ściana boczna jest nachylona do płaszczyzny
podstawy pod kątem 60 stopni, a krawędź boczna ma 5. Oblicz objętość.
2. Dany jest ostrosłup prawidłowy sześciokątny, krawędź boczna jest nachylona do podstawy pod
kątem, którego cos=2/3. Suma długości wszystkich krawędzi ostrosłupa jest równa 60. Wyznacz
długość krawędzi.
Naprawdę nie ogarniam tych zadań

POMÓŻCIE, PROSZĘ
20 lis 19:59
dero2005:
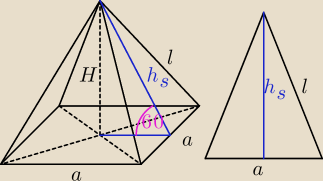
l = 5
l
2 = h
s2 + (
a2)
2
z drugiego równania
wstawiamy do pierwszego
(
hs2)
2 + h
s2 = l
2
5h
s2 = 100
h
s2 = 20
h
s = 2
√5
a2 =
√5
a = 2
√5
H =
√15
20 lis 21:28
dero2005:
6a + 6l = 60 ⇒ l = 10 − a → wstawiamy do trzeciego
l
2 = (
a2)
2 + h
s2
| | a√3 | |
h = |
| ⇒ wstawiamy do pierwszego |
| | 2 | |
| a√3 | | 2 | | 3 | |
| = |
| ⇒ hs = |
| a√3 → wstawiamy do trzeciego |
| 2hs | | 3 | | 4 | |
| | a2 | | 27 | |
(10−a)2 = |
| + |
| a2 |
| | 4 | | 16 | |
| | a2 | | 27 | |
100 − 20a + a2 = |
| + |
| a2 |
| | 4 | | 16 | |
po rozwiązaniu równania, które zalecam wykonać wychodzi
20 lis 21:54
Kinga: dziękuję za pomoc dero2005

21 lis 17:09
Wiola: 1. Przekrój osiowy stożka jest trójkątem równobnocznym, którego bok ma długość 4 cm. Oblicz
objętość i pole boczne stożka.
2. Przekrój osiowy walca jest kwadratem o przekątnej długości 2 √3 cm. Oblicz objętość i
pole całkowite walca.
3. Oblicz objętość kuli o polu powierzchni 16π.
4. Pole całkowite walca wynosi 785 cm2, pole boczne wynosi 628 cm2. Oblicz objętość walca.
5. Równoległobok o bokach długości 5 cm i 3 cm oraz kącie ostrym 60℃ obraca się wokół dłuższego
boku. Oblicz objętość i pole całkowite tej bryły.
Proszę o pomoc w rozwiązaniu tych zadań w jak najprostszy sposób.
3 gru 20:01
mariusz: podstawą prostopadłościanu jest prostokąt o bokach 6cm i 8cm,a tangens kąta nachylenia
przekątnej tego prostopadłościanu do podtawy wynosi 1,6cm.Oblicz objętość tego
prostopadłościanu
8 gru 11:03
dero2005:
d = l = 4
8 gru 11:33
dero2005:
D = 2
√3
8 gru 11:38
dero2005:
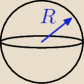
S = 4πR
2 = 16π
R = 2
8 gru 11:41
dero2005:
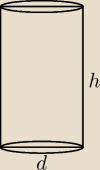
P
b = πdh = 628
πd
2 = 314
| | πd2 | | 157 | |
V = |
| *h = |
| √314π ≈ 1570 cm3 |
| | 4 | | π | |
8 gru 12:01
dero2005:
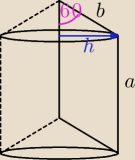
a = 5
b = 3
P
c = 2πh(a+b) = 24π cm
2
8 gru 12:16
dero2005:
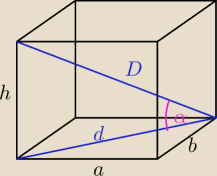
a = 8 cm
b = 6 cm
d =
√a2 + b2 = 10 cm
h = d*tgα = 160 cm
V = a*b*h = 7680 cm
3
8 gru 12:23
sssss3:
15 gru 15:21
Kamilo: pomocy w zadaniu dla mnie to czarna mamba

Długość krawędzi podstawy ostrosłupa
prawidłowego trójkątnego wynosi 12 cm . Ściana boczna
ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 60°. Oblicz objętość tego ostrosłupa oraz
pole powierzchni całkowitej.
15 gru 16:57
dero2005:
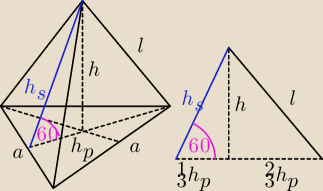
a = 12
h
s = 4
√3
h =
√hs2 − (13hp)2 = 2
√6
P
c = P
p + P
b = 108
√3
15 gru 20:20
xD: ♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦
♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥♦♠♣♥
17 gru 16:48
kamil: w prostopaloscianie krawedzie podstawy maja 6 i 8 przekatna tworzy z plaszczyzna kat 30 stopni.
Oblicz pole powierzchni bocznej
18 gru 12:44
dero2005:
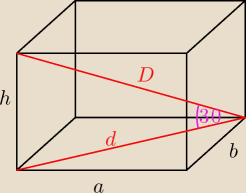
a = 8
b = 6
d =
√a2 + b2 =
P
b = 2h(a+b) =
18 gru 18:33
jola:
29 gru 15:17
jola: oblicz objętość ostrosłupa prawidłowego trójkątnego którego podstawa ma długość 4cm a wysokość
ostrosłupa wynosi 15 cm
29 gru 15:21
jola: bardzo proszę o pomoc w rozwiązaniu
29 gru 15:22
29 gru 15:23
teresa:
function(){return this[this.length-1]}
9 sty 19:40
Paula: 1. na kwadracie opisano drugi kwadrat w taki sposób, ze w srodku kazego jego boku o dlugosci 24
cm leza wierzchołki mniejszego kwadratu. Oblicz pole i obwód kwadratu wpisanego. Moglby mi
ktos to objaśnić :")
Paula
12 sty 00:19
Paula: 1.Kwadrat i prostokąt mają jednakowe pola. Oblicz pole kwadratu, jezeli jeden bok prostokąta
jest o 2 cm krotszy a drugi bok jest o 6 cm dluzszy od boku kwadratu.
2. Oblicz pole prostokąta, którego przekatne maja 18 cm dlugosci, a kat miedzy nimi ma miare
120 stopni.
3. Oblicz pole prostokąta, w którym kąt miedzy przekątnymi wynosi 120 stopni, a dluzszy bok
wynosi 24 cm.
4. O ile procent zwiekszy sie pole prostokąta, jezeli dlugosc jednego boku zwiekszy sie o 20 %,
a dlugosc drugiego boku o 15 %?
5. w trapezie prostokątnym o podstawach długości 21 cm i 12 cm , ramie nie bedace wysokoscia
wynosi 15 cm. jakiej dlugosci sa przekatne trapezu?
12 sty 00:26
Paula: bardzo prosze o pomoc w rozwiazaniu tych zadan.

12 sty 00:27
dero2005:
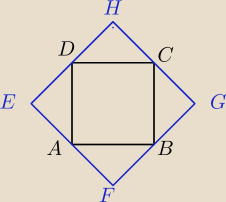 EF = FG = GH = HE = 24 cm
EF = FG = GH = HE = 24 cm
DC
2 = HC
2 + HD
2
DC =
√288 = 12
√2
P = DC
2 = 288 cm
2 ⇒ pole
O = 4*DC = 48
√2 cm ⇒ obwód
12 sty 12:24
dero2005:
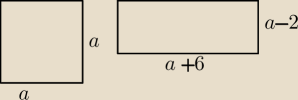
zad1
P
k = P
p
a
2 = (a+6)(a−2)
a
2 = a
2 − 2a + 6a −12
4a = 12
a = 3
P
k = a
2 = 9
12 sty 12:31
dero2005:
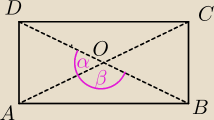
zad 2
AC = DB = 18
β = 120
o
α + β = 180
o
α = 180−120 = 60
o
ponieważ AO = DO = 9 i kąt α = 60
o to Δ
AOD jest równoboczy i AD = 9
z tw Pitagorasa:
AB =
√BD2 − AD2 =
√182 − 92 =
√405 = 9
√5
pole
P = AB*AD = 9*9
√5 = 81
√5 cm
2
12 sty 12:45
dero2005:
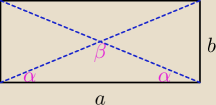
zad 3
a = 24 cm
β = 120
o
2α + β = 180
o suma kątów trójkąta
2α = 180−120 = 60
o
α = 30
o
b = 8
√3 cm
P =a*b = 192
√3 cm
2
12 sty 12:51
dero2005:
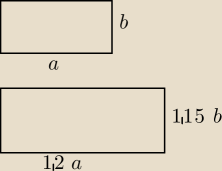
zad 4
| (1,2a*1,15b) − (a*b) | | 1,38ab − ab | | ab(1,38−1) | |
| *100 % = |
| *100% = |
| * 100% = 38% |
| (a*b) | | ab | | ab | |
12 sty 12:59
dero2005:
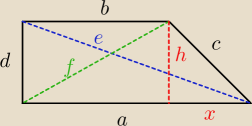
zad 5
dane
a = 21 cm
b = 12 cm
c = 15 cm
x = a−b = 9
z tw Pitagorasa
h =
√c2 − x2 = 12
d = h = 12 cm
z tw Pitagorasa
e =
√a2 + d2 =
√585 = 3
√65
f =
√b2 + d2 =
√288 = 12
√2
12 sty 13:23
anna:
12 sty 17:40
Ricia : W trapezie rownoramiennym wieksza podstawa ma dlugosc 10pierwiastkow3 a przekatna ma dlugosc
15, a kat przy podstawie ma miare 60 stopni. Oblicz dlugosc ramienia trapezie
12 sty 17:51
Ricia : Półkole o promieniu r zwinieto w powierzchnie stożkowa. Wyznacz kat rozwarcia oraz objętość
tego stozka
12 sty 17:52
Ricia : W trójkącie prostokątnym punkt styczności okręgu wpisanego w ten trojkat dzieli
przeviwprostokatna na odcinki długości 5 i 12 . Oblicz długości przyprostokatnych trojkata
Odpowiedz powinna byc 8 i 15

12 sty 17:54
Ricia : dlugosci trzech kolejnch bokow czworokata opisanego na okreg tworza ciag arytmetyczny. obowd
tego czworokata rowna sie 81,6. najmniejszy bok ma dlugosc rowna 66 2/3% dlugosci
największego. Oblicz dlugosci bokow tego czworokata
12 sty 18:10
dero2005:
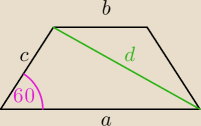
a = 10
√3
d = 15
d
2 = a
2+c
2 − 2a*c*cos60
o
c
2 − 10
√3c + 75 = 0
Δ = 0
c = 5
√3
12 sty 18:14
dero2005:
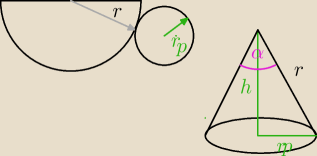
(r
p)
2 = 2r
2 − 2r
2cosα
r
2 = 2r
2 − 2r
2cosα
α = arc cos
12 = 60
o
12 sty 18:27
dero2005:
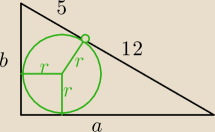
a = r + 12
b = r + 5
c = 5+12 = 17
a
2 + b
2 = 17
2
(r + 12)
2 + (r + 5)
2 = 289
po rozwiązaniu
r = 3
r = −20 → odrzucamy
a = 3 + 12 = 15
b = 3 + 5 = 8
12 sty 18:41
Ricia : Oblicz dlugosci przekatnych rownolegloboku zbudowanego na wektorach a=2P+q b=P−2q gdIe P i q sa
wektorami jednostkowymi i kat miedzy nimi ma miare pi/3
12 sty 18:45
Ricia : Dziekuje ślicznie, matematyka stała sie jut trochę jaśniejsze

12 sty 18:45
asia: dany jest kwadrat o przekątnej długości 8 cm. z wierzchołka kwadratu zakreslamy koło o
promieniu równym dlugości boku kwadratu. pp części wspolnej kwadratu i kola jest równe
13 sty 13:25
mila: Z1. Długościami boków trójkąta mogą byc:
A.√27,√48,√75
B. 6mm , 0,1dm , 12cm
C. 4,2−√3,2 +√3
D. 2dm , 4cm, 0,07 m
13 sty 13:38
mila: z2. W trójkącie równoramiennym kąt przy podstawie ma miarę o 30stopni od miary kąta między
ramionami . Kąt miedzy ramionami ma miare?
13 sty 13:43
dero2005:
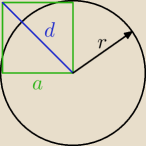
d = 8
r = a = 4
√2
13 sty 17:05
emila: liczba log36 jest równa
18 lut 12:44
ratunku : Pokaż wyniki wyszukiwania frazy "ile jest wszystkich liczb naturalnych dwucyfrowych w ktorych
obie cyfry sa parzyste a.16 , b.20 .c.24 . d.25"
18 lut 12:50
maksi123:
jakie są figury płaskie
24 lut 16:26
maksi123: jakie są figury płaskie
24 lut 16:28
Sandra: Część chciałabym żebyś mi pomógł/a =P
To są zadania ... =D
Zad1. Oblicz pole powierzchni graniastosłupa prawidłowego trójkątnego,którego krawędź podstawy
ma długość 5√3 cm2,a krawędź boczna 15cm.
Zad2. Pole boczne graniastosłupa prawidłowego trójkątnego wynosi 234cm2,a krawędź podstawy ma
długość 6cm. Oblicz pole całkowite i objętości.
Zad3. W ostroslupie prawidłowym czworokatnym przekątna podstawy o dlugosci 12√2 cm tony z
krawędzią boczna 45 stopni . Oblicz objętość.
26 maj 07:43
Sandra: Zad1 Oblicz pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego,którego
krawędź podstawy ma długość 6√3 cm,a krawędź boczna 12cm.
Zad2. Oblicz objętość i pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego
jeżeli krawędź podstawy ma długość 5cm a pole powierzchni całkowitej jest równa 276cm2.
Zad3. W ostroslupie prawidłowym wysokość ściany bocznej o długości 8√3 cm tworzy z wysokością
ostrosłupa kat 30 stopni. Oblicz objętość tego ostrosłupa.
Dziękuję za rozwiązanie zadań =D=D
26 maj 08:01
Monia: Jedna z przekątnych graniastosłupa prostego ma długość 10 cm i nachylona jest do podstawy pod
kątem 30 stopni. Oblicz wysokość tego graniastosłupa. Zad 2 Ile litrów wody zmieści się w
beczce, która ma kształt walca o średnicy 60 cm i wysokości 0,9m. Zad3 Do pięciu danych :1,
2, 3, 4, 5 dopisano taką szóstką liczbę x, mediana tych 6 danych jest równa ich modzie. Znajdz
liczbę x. Zad 4 Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest kwadratem o
polu powierzchni 64 cm sześciennych. Oblicz pole powierzchni podstawytego walca. Wynik podaj z
dokładnością do 0,01.
20 mar 18:52
Angel : Oblicz pole stazka o kacie rozwarcia rownym 60 ℃ i wysokosc o dlugisci 5 ∫3 .
Wykonaj rysunek i zapisz odpowiednie ozbaczenia .
7 cze 11:43
 dane
a = 5
h = 2
podstawa − trójkąt równoboczny
dane
a = 5
h = 2
podstawa − trójkąt równoboczny
 dane
a = 3√2
L = 2(2a+c)+3h = 18(√2+6)
c2 = a2+a2 = 2a2 = 2*18 = 36
c = 6 przeciwprostokątna
L = 4a+2c+3h
3h = L − 4a − 2c = 18√2 + 108 − 12√2 − 12 = 6√2 + 96
dane
a = 3√2
L = 2(2a+c)+3h = 18(√2+6)
c2 = a2+a2 = 2a2 = 2*18 = 36
c = 6 przeciwprostokątna
L = 4a+2c+3h
3h = L − 4a − 2c = 18√2 + 108 − 12√2 − 12 = 6√2 + 96
 dane
f = 16 cm
d = 12 cm
l = 15 cm
tw. Pitagorasa
(d2)2 + (f2)2 = a2
62 + 82 = a2
100 = a2
a = 10 cm krawędź podstawy
h = √l2 − a2 = √225−100 = √125 = 5√5 cm wysokość
Pp = 12df = 16*122 = 96 cm2 powierzchnia podstawy
Pc = 2*Pp + 4*ah = 2*96 + 4*10*5√5 = 192 + 200√5 cm2 pow całkowita
V = Pp*h = 96*5√5 = 480√5 cm3 objętość
dane
f = 16 cm
d = 12 cm
l = 15 cm
tw. Pitagorasa
(d2)2 + (f2)2 = a2
62 + 82 = a2
100 = a2
a = 10 cm krawędź podstawy
h = √l2 − a2 = √225−100 = √125 = 5√5 cm wysokość
Pp = 12df = 16*122 = 96 cm2 powierzchnia podstawy
Pc = 2*Pp + 4*ah = 2*96 + 4*10*5√5 = 192 + 200√5 cm2 pow całkowita
V = Pp*h = 96*5√5 = 480√5 cm3 objętość
 d2 = 82 + 62 = 64+36 = 100
d =√100 = 10
d2 = 82 + 62 = 64+36 = 100
d =√100 = 10
 dane
d = 10 dm
dane
d = 10 dm


 3)
D = 8√2
α = 60o
dD = cos α = cos 60o = 12
3)
D = 8√2
α = 60o
dD = cos α = cos 60o = 12
 D = 4 dm
α = 60o
D = 4 dm
α = 60o
 zad 5)
a = 8 cm
zad 5)
a = 8 cm



 a o które zadanie chodzi?
a o które zadanie chodzi?
 .
.
 ..czyli Pb rombu to bd, Pb=4ah? i tak z kazda figura tyle ile scian to razy tyle
mnozymy a z h?
..czyli Pb rombu to bd, Pb=4ah? i tak z kazda figura tyle ile scian to razy tyle
mnozymy a z h? .. a jak bym nie mial "a" lub "h" to jak je wyznaczyc?
.. a jak bym nie mial "a" lub "h" to jak je wyznaczyc?

 już tłumaczę
d − przekątna podstawy (kwadratu)
z Pitagorasa
a2 + a2 = d2
2a2 = d2
już tłumaczę
d − przekątna podstawy (kwadratu)
z Pitagorasa
a2 + a2 = d2
2a2 = d2
 teraz juz rozumiem. A ten wzro h = √D2 − d2 = 4√6 to jest na wysokosc rombu? i dlaczeg
ow zadaniu 3 i 5 wzory na male "d" sa rozne? i dlaczego w zadaniu 5 oczywiscie tej drugiej
listy zadań Pp − wystepuje sin?
teraz juz rozumiem. A ten wzro h = √D2 − d2 = 4√6 to jest na wysokosc rombu? i dlaczeg
ow zadaniu 3 i 5 wzory na male "d" sa rozne? i dlaczego w zadaniu 5 oczywiscie tej drugiej
listy zadań Pp − wystepuje sin?
 .
Bo z tymi "L" to wgl. sie pogubilem o co tam chodzi
.
Bo z tymi "L" to wgl. sie pogubilem o co tam chodzi
 . A mogłbys jeszcze na te zadanka spojrzeć? i pokazać mi jak to się
je rozwiązuje krok po kroku?
. A mogłbys jeszcze na te zadanka spojrzeć? i pokazać mi jak to się
je rozwiązuje krok po kroku? zad1. Wysokość ostrosłupa prawidłowego jest równa 3, a jego podstawą jest kwadrat o boku 4√2.
Narysuj siatkę tego ostroslupa i oblicz jesgo pole powierzchni calkowitej.
zad2. Podstawą ostrosłupa jest kwadrat ABCD o boku długosći 6. Ściana boczna ABS jest
prostopadła do podstawy oraz |AS|=|BS|=5. Narysuj siatkę tego ostrosłupa i oblicz jego pole
powierzchni calkowitej.
zad3. Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe polu jego podstawy.
Oblicz sinus kąta naychlenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
zad4. Wysokosć ostrosłupa prawidłowego trójkątnego jest równa √3, a kąt nachylenia ściany
bocznej do płaszczyzny podstawy ma miarę 30(stopni). Oblicz objętość i pole powierzchni
bocznej tego ostrosłupa.
zad5. Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny
podstawy pod kątem 30(stopni), a jej wysokość jest równa 3√3. Oblicz objętość tego
ostrosłupa.
zad6. Podstawą ostroslupa o wierzchołku S jest trójkąt ABC o bokach długości: |AB|=6, |AC|=
|BC|= 5. Wysokość ostrosłupa jest równa 2, a jej spodek jest środkiem okręgu opisanego na
podstawie. Oblicz tangens kąta nachylenia ściany ABS do płaszczyzny podstawy ostrosłupa.
zad7. Ostrosłupa prawidłowy czworokątny, którego krawędź boczna ma długość 5, a przekątna
podstawy 8, przecieto płaszczyznę równoległą do podstawy, przechodzącą przez środek jesgo
wysokości. Oblicz bojętość części, na które ta płaszczyzna podzieliła ostrosłup.
zad1. Wysokość ostrosłupa prawidłowego jest równa 3, a jego podstawą jest kwadrat o boku 4√2.
Narysuj siatkę tego ostroslupa i oblicz jesgo pole powierzchni calkowitej.
zad2. Podstawą ostrosłupa jest kwadrat ABCD o boku długosći 6. Ściana boczna ABS jest
prostopadła do podstawy oraz |AS|=|BS|=5. Narysuj siatkę tego ostrosłupa i oblicz jego pole
powierzchni calkowitej.
zad3. Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe polu jego podstawy.
Oblicz sinus kąta naychlenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
zad4. Wysokosć ostrosłupa prawidłowego trójkątnego jest równa √3, a kąt nachylenia ściany
bocznej do płaszczyzny podstawy ma miarę 30(stopni). Oblicz objętość i pole powierzchni
bocznej tego ostrosłupa.
zad5. Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny
podstawy pod kątem 30(stopni), a jej wysokość jest równa 3√3. Oblicz objętość tego
ostrosłupa.
zad6. Podstawą ostroslupa o wierzchołku S jest trójkąt ABC o bokach długości: |AB|=6, |AC|=
|BC|= 5. Wysokość ostrosłupa jest równa 2, a jej spodek jest środkiem okręgu opisanego na
podstawie. Oblicz tangens kąta nachylenia ściany ABS do płaszczyzny podstawy ostrosłupa.
zad7. Ostrosłupa prawidłowy czworokątny, którego krawędź boczna ma długość 5, a przekątna
podstawy 8, przecieto płaszczyznę równoległą do podstawy, przechodzącą przez środek jesgo
wysokości. Oblicz bojętość części, na które ta płaszczyzna podzieliła ostrosłup.
 zad1)
dane:
a = 4√2 − krawędź podstawy
h = 3 − wysokość ostrosłupa
oznaczenia:
d − przekątna podstawy (kwadratu)
hs − wysokość ściany bocznej (trójkąta)
l − krawędź boczna (ramię trójkąta równoramiennego o podstawie a)
Z trójkąta prostokątnego liczymy hs wg tw. Pitagorasa
hs2 = (a2)2 + h2 = (4√22)2 + 32 = (2√2)2 + 9 = 8 + 9 = 17
hs = √17
Pp − pole podstawy (pole kwadratu)
Pp = a2 = (4√2)2 = 32
Ps − pole ściany bocznej (pole trójkąta)
zad1)
dane:
a = 4√2 − krawędź podstawy
h = 3 − wysokość ostrosłupa
oznaczenia:
d − przekątna podstawy (kwadratu)
hs − wysokość ściany bocznej (trójkąta)
l − krawędź boczna (ramię trójkąta równoramiennego o podstawie a)
Z trójkąta prostokątnego liczymy hs wg tw. Pitagorasa
hs2 = (a2)2 + h2 = (4√22)2 + 32 = (2√2)2 + 9 = 8 + 9 = 17
hs = √17
Pp − pole podstawy (pole kwadratu)
Pp = a2 = (4√2)2 = 32
Ps − pole ściany bocznej (pole trójkąta)
 siatka ostrosłupa do zad 1
siatka ostrosłupa do zad 1
 zad 2)
dane:
a = |AB| = |BC| = |CD| = |AD|
a = 6
|BS| = |AS| = 5
liczymy wysokość trójkąta ABS
h = √|AS|2 − (a2)2 = √52 − 32 = √25−9 = √16 = 4
liczymy powierzchnię trójkąta ABS
zad 2)
dane:
a = |AB| = |BC| = |CD| = |AD|
a = 6
|BS| = |AS| = 5
liczymy wysokość trójkąta ABS
h = √|AS|2 − (a2)2 = √52 − 32 = √25−9 = √16 = 4
liczymy powierzchnię trójkąta ABS
 siatka do zad 2)
rysujemy kwadrat o boku a, następnie cyrklem z punktu A i B zakreślamy długości |BS|=|AS|,
z punktów C i D zakreślamy odcinki |CS| = |DS|. W ten sposób znajdujemy punty S
Na rysunku nie jest to proporcjonalne bo nie miałem cyrkla, jest to tylko rysunek poglądowy
siatka do zad 2)
rysujemy kwadrat o boku a, następnie cyrklem z punktu A i B zakreślamy długości |BS|=|AS|,
z punktów C i D zakreślamy odcinki |CS| = |DS|. W ten sposób znajdujemy punty S
Na rysunku nie jest to proporcjonalne bo nie miałem cyrkla, jest to tylko rysunek poglądowy
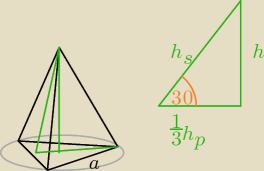 Zad4)
dane:
h = √3
α = 30o
oznaczenia
hs − wysokość ściany bocznej
hp − wysokość podstawy
a − krawędź podstawy
Zad4)
dane:
h = √3
α = 30o
oznaczenia
hs − wysokość ściany bocznej
hp − wysokość podstawy
a − krawędź podstawy
 Zad 5)
dane
hs = 3√3 wysokość ściany bocznej
α = 30o nachylenie ściany
oznaczenia
a − krawędź podstawy
h − wysokość ostrosłupa
hp − odległość spodka wysokości od krawędzi
Zad 5)
dane
hs = 3√3 wysokość ściany bocznej
α = 30o nachylenie ściany
oznaczenia
a − krawędź podstawy
h − wysokość ostrosłupa
hp − odległość spodka wysokości od krawędzi
 zad 6)
dane
|AB| = 6
|AC| = 5
|BC| = 5
h = 2
h1 = √52 − 32 = √25−9 = √16 = 4 wysokość podstawy
zad 6)
dane
|AB| = 6
|AC| = 5
|BC| = 5
h = 2
h1 = √52 − 32 = √25−9 = √16 = 4 wysokość podstawy
 . z gory dzieki
. z gory dzieki
 . z gory dzieki
. z gory dzieki
 . z gory dzieki
. z gory dzieki
 dane
|AC| = d = 8 − przekątna podstawy
|CS| = l = 5 − krawędź boczna
liczymy a − krawędź podstawy
2a2 = d
2a2 = 8
a2 = 4
a = 2
liczymy h − wysokość ostrosłupa |OS| z trójkąta OCS
h = √l2 − (d2)2 = √52 − 42 = √25−16 = √9 = 3
liczymy objętość ostrosłupa ABCDS
V = 13a2*h = 13*22*3 = 4
liczymy |O'E'| z podobieństwa trójkątów OES i O'E'S
dane
|AC| = d = 8 − przekątna podstawy
|CS| = l = 5 − krawędź boczna
liczymy a − krawędź podstawy
2a2 = d
2a2 = 8
a2 = 4
a = 2
liczymy h − wysokość ostrosłupa |OS| z trójkąta OCS
h = √l2 − (d2)2 = √52 − 42 = √25−16 = √9 = 3
liczymy objętość ostrosłupa ABCDS
V = 13a2*h = 13*22*3 = 4
liczymy |O'E'| z podobieństwa trójkątów OES i O'E'S
 . za pomoc
. za pomoc
 zad1. Dany jest prostokat mający boki 4cm i 8cm. Środki boków prostokąta są wierzchołkami
rombu. Wyznacz pole tego rombu.
zad2. Wysokość trójkąta równobocznego wynosi 2√3. Wyznacz jego obwód.
zad3. Liczby 8,15,x są długościami boków trójkąta prostokątnego. wyznacz x.
zad4. Podstawy trapezu równoramiennego mają długość 10cm i 12cm a ramię ma długość 4cm. Oblicz
pole tego trapezu.
zad5. Przekątna kwadratu jest równa P{5}. Oblicz obwód tego kwadratu.
zad6. Dłuższa przyprostokątna trójkąta prostokątnego ma długość 9, a jeden z kątów ostrych
30(stopni). Wyznacz pole tego trójkąta.
zad1. Dany jest prostokat mający boki 4cm i 8cm. Środki boków prostokąta są wierzchołkami
rombu. Wyznacz pole tego rombu.
zad2. Wysokość trójkąta równobocznego wynosi 2√3. Wyznacz jego obwód.
zad3. Liczby 8,15,x są długościami boków trójkąta prostokątnego. wyznacz x.
zad4. Podstawy trapezu równoramiennego mają długość 10cm i 12cm a ramię ma długość 4cm. Oblicz
pole tego trapezu.
zad5. Przekątna kwadratu jest równa P{5}. Oblicz obwód tego kwadratu.
zad6. Dłuższa przyprostokątna trójkąta prostokątnego ma długość 9, a jeden z kątów ostrych
30(stopni). Wyznacz pole tego trójkąta.

 , a mozesz jeszcze te zrobic? bo chce sprawdzic czy dobrze je sam rozwiazalem
, a mozesz jeszcze te zrobic? bo chce sprawdzic czy dobrze je sam rozwiazalem .
zad1. Wyznacz miarę kąta ostrego rombu którego pole jest rowne 24√3 a jego wysokosc 6.
zad2. Wyznacz promień okręgu wpisanego w trójkat równoboczny o boku 6.
zad3. Przekątna prostokata o długości 10cm tworzy z dłuższym bokiem kąt 30(stopni). Wyznacz
pole tego prostokąta.
zad4. Obwód trójkąta równobocznego jest równy 32cm. Podstawa tego trójkąta jest o 1 cm dłuższa
od ramienia. Wyznacz długość ramienia tego trójkąta.
zad5. Oblicz pole równoległoboku o bokach długości 1 dm i 4cm oraz kącie rozwartym o mierze
140(stopni).
zad6. Wyznacz równanie okręgu o środku S (−1,3) i promieniu 4.
.
zad1. Wyznacz miarę kąta ostrego rombu którego pole jest rowne 24√3 a jego wysokosc 6.
zad2. Wyznacz promień okręgu wpisanego w trójkat równoboczny o boku 6.
zad3. Przekątna prostokata o długości 10cm tworzy z dłuższym bokiem kąt 30(stopni). Wyznacz
pole tego prostokąta.
zad4. Obwód trójkąta równobocznego jest równy 32cm. Podstawa tego trójkąta jest o 1 cm dłuższa
od ramienia. Wyznacz długość ramienia tego trójkąta.
zad5. Oblicz pole równoległoboku o bokach długości 1 dm i 4cm oraz kącie rozwartym o mierze
140(stopni).
zad6. Wyznacz równanie okręgu o środku S (−1,3) i promieniu 4.

 . Jak nie mozesz ich rozwiazac to
ok, pojde do kolegi zeby mi w tym pomogl
. Jak nie mozesz ich rozwiazac to
ok, pojde do kolegi zeby mi w tym pomogl
 zad 1)
P = a*h = 24√3
zad 1)
P = a*h = 24√3
 zad5)
α = 180 − 140 = 40 o
h4 = sin 40o = 0,6427
h = 4* 0,6427 = 2,57 cm
P = a*h = 10 * 2,57 = 25,7 cm2
zad5)
α = 180 − 140 = 40 o
h4 = sin 40o = 0,6427
h = 4* 0,6427 = 2,57 cm
P = a*h = 10 * 2,57 = 25,7 cm2

 . taka tresc zadania w szkole dostalem: "Obwód trójkąta równobocznego jest równy
32cm. Podstawa tego trójkąta jest o 1 cm dłuższa
od ramienia. Wyznacz długość ramienia tego trójkąta."
. taka tresc zadania w szkole dostalem: "Obwód trójkąta równobocznego jest równy
32cm. Podstawa tego trójkąta jest o 1 cm dłuższa
od ramienia. Wyznacz długość ramienia tego trójkąta."

 przyjmuję wstępnie ,że jest to trójkąt równoramienny
przyjmuję wstępnie ,że jest to trójkąt równoramienny
 . dzioeki
. dzioeki

 tw Pitagorasa
a2 + a2 = d2
2a2 = d2
a2 = d22
tw Pitagorasa
a2 + a2 = d2
2a2 = d2
a2 = d22
 A moglbys jeszcze na to zerknać? powinno wyjsc 288cm3. ale nie wychodzi cos
A moglbys jeszcze na to zerknać? powinno wyjsc 288cm3. ale nie wychodzi cos zad. Oblicz objetość ostrosłupa prawidłowego trójkątnego, w którym wysokość jest równa 24 a
wysokość
ściany bocznej wynosi 26.
zad. Oblicz objetość ostrosłupa prawidłowego trójkątnego, w którym wysokość jest równa 24 a
wysokość
ściany bocznej wynosi 26.

 H = 24
h = 26
1.
długość krawędzi podstawy:
H = 24
h = 26
1.
długość krawędzi podstawy:

 CZesc.
Czy potrafil by mi ktos rozwiazac te zadanka, bo jutro z tego musze zaliczyc semestr...
rysunek jest do zadania 5.
zad.1
Oblicz objetosc i pole powierzchni calkowitej czworoscianu foremnego ktorego krawedz ma dlugosc
6√2
zad.2
Onlicz objetosc ostrosłupa prawidłowego trójkatnego, w ktorym wysokosc jest rowna 24, a
wysokosc sciany bocznej wynosi 26
zad.3
Oblicz pole powierzchni i objetosc ostrosłupa prawidłowego czworokatnego, ktorego krawedz
podstawy ma długosc 5 a krawedz boczna 8.
zad.4
Podstawa ostrosłupa jest trójkat prostokatny o przyprostokatnych 16 i 12. Kazda krawedz boczna
ostrosłupa jest nachylona do płaszczyzny podstawy po katem 60stopni. Oblicz objetosc
ostrosłupa.
zad.5
rys:(tam gdzie jest czerwona kropka na dole jest 12, a tam gdzie jest kropka z boku jest 14)
Wyznacz objetosc i pole powierzchni calkowitej ostroslupa prawidlowego trojkatnego.
CZesc.
Czy potrafil by mi ktos rozwiazac te zadanka, bo jutro z tego musze zaliczyc semestr...
rysunek jest do zadania 5.
zad.1
Oblicz objetosc i pole powierzchni calkowitej czworoscianu foremnego ktorego krawedz ma dlugosc
6√2
zad.2
Onlicz objetosc ostrosłupa prawidłowego trójkatnego, w ktorym wysokosc jest rowna 24, a
wysokosc sciany bocznej wynosi 26
zad.3
Oblicz pole powierzchni i objetosc ostrosłupa prawidłowego czworokatnego, ktorego krawedz
podstawy ma długosc 5 a krawedz boczna 8.
zad.4
Podstawa ostrosłupa jest trójkat prostokatny o przyprostokatnych 16 i 12. Kazda krawedz boczna
ostrosłupa jest nachylona do płaszczyzny podstawy po katem 60stopni. Oblicz objetosc
ostrosłupa.
zad.5
rys:(tam gdzie jest czerwona kropka na dole jest 12, a tam gdzie jest kropka z boku jest 14)
Wyznacz objetosc i pole powierzchni calkowitej ostroslupa prawidlowego trojkatnego.
 czy to jest graniastosłup prawidłowy? tzn czy podstawa jest kwadratem? Zakładam , że tak.
D = 9 cm
Pp = a2 = 16 cm2
a = √16 = 4 cm
d = a√2 = 4√2 cm
h = √D2 − d2 = √81 − 32 = √49 = 7 cm
V = Pp*h = 16*7 = 112 cm3
czy to jest graniastosłup prawidłowy? tzn czy podstawa jest kwadratem? Zakładam , że tak.
D = 9 cm
Pp = a2 = 16 cm2
a = √16 = 4 cm
d = a√2 = 4√2 cm
h = √D2 − d2 = √81 − 32 = √49 = 7 cm
V = Pp*h = 16*7 = 112 cm3
 oblicz pole siatki ostros8,5cm i 10cmupa
oblicz pole siatki ostros8,5cm i 10cmupa
 h = 4√3
h = 4√3
 Oblicz objętość
Oblicz objętość
 zad 1
zad 1
 a = 5
l = 8
d = a√2 = 5√2
a = 5
l = 8
d = a√2 = 5√2
 D = 9
m = a√3
D = 9
m = a√3
 h = 2r = 8
h = 2r = 8
 r = 1
h = 2r = 2
r = 1
h = 2r = 2
 b = 6 dm
b = 6 dm
 OB = OC = 10
BD = GF = 8
DO = √102−82 = 6
DC = OC − OD = 10−6 = 4
CB = √DB2 + DC2 = √82 + 42 = √80 = 4√5
GO = DO = 6
GC = GO + OC = 6 + 10 = 16
FC = √GF2 + GC2 = √82 + 162 = √320 = 8√5
OB = OC = 10
BD = GF = 8
DO = √102−82 = 6
DC = OC − OD = 10−6 = 4
CB = √DB2 + DC2 = √82 + 42 = √80 = 4√5
GO = DO = 6
GC = GO + OC = 6 + 10 = 16
FC = √GF2 + GC2 = √82 + 162 = √320 = 8√5
 AB = BC = CD = a = 12
AB = BC = CD = a = 12
 h = 5a
Pc = 2a2 + 4ah = 500
2a2 + 4*a*5a = 500
22a2 = 500
h = 5a
Pc = 2a2 + 4ah = 500
2a2 + 4*a*5a = 500
22a2 = 500
 c = h
a = b
2a + c = 12 + 6√2
2a2 = c2
rozwiąż układ równań, policzyć a, b=a , c = h
c = h
a = b
2a + c = 12 + 6√2
2a2 = c2
rozwiąż układ równań, policzyć a, b=a , c = h
 hp = 6 cm
hp = 6 cm

 zad1
a = 10
H = 1,2a = 12
hs = √H2 + (a2)2 = √122 + 52 = √169 = 13
Pp = a2 + 2a*hs =
zad1
a = 10
H = 1,2a = 12
hs = √H2 + (a2)2 = √122 + 52 = √169 = 13
Pp = a2 + 2a*hs =
 r = 8
h = 2r = 16
Pc = 2πr(r + h) =
V = πr2*h =
r = 8
h = 2r = 16
Pc = 2πr(r + h) =
V = πr2*h =
 na serio tego nie ogarniam
na serio tego nie ogarniam
 D = 24
D = 24
 zad1
a = 2
zad1
a = 2
 zad 2 " i jest nachylona ( do czego ?) pod kątem"
D = 8
zad 2 " i jest nachylona ( do czego ?) pod kątem"
D = 8
 zad 4
a = 6
b = 2
zad 4
a = 6
b = 2
 a = 3√3
b = 6
α = 30o
a = 3√3
b = 6
α = 30o
 POMÓŻCIE, PROSZĘ
POMÓŻCIE, PROSZĘ
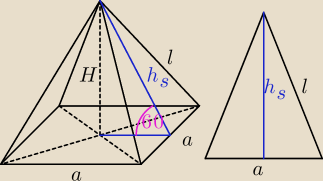 l = 5
l2 = hs2 + (a2)2
l = 5
l2 = hs2 + (a2)2


 d = l = 4
d = l = 4
 D = 2√3
D = 2√3
 S = 4πR2 = 16π
R = 2
S = 4πR2 = 16π
R = 2
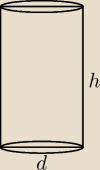
 a = 5
b = 3
a = 5
b = 3
 a = 8 cm
b = 6 cm
a = 8 cm
b = 6 cm
 Długość krawędzi podstawy ostrosłupa
prawidłowego trójkątnego wynosi 12 cm . Ściana boczna
ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 60°. Oblicz objętość tego ostrosłupa oraz
pole powierzchni całkowitej.
Długość krawędzi podstawy ostrosłupa
prawidłowego trójkątnego wynosi 12 cm . Ściana boczna
ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 60°. Oblicz objętość tego ostrosłupa oraz
pole powierzchni całkowitej.
 a = 12
a = 12
 a = 8
b = 6
d = √a2 + b2 =
a = 8
b = 6
d = √a2 + b2 =

 EF = FG = GH = HE = 24 cm
EF = FG = GH = HE = 24 cm
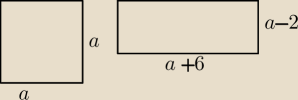 zad1
Pk = Pp
a2 = (a+6)(a−2)
a2 = a2 − 2a + 6a −12
4a = 12
a = 3
Pk = a2 = 9
zad1
Pk = Pp
a2 = (a+6)(a−2)
a2 = a2 − 2a + 6a −12
4a = 12
a = 3
Pk = a2 = 9
 zad 2
AC = DB = 18
β = 120o
α + β = 180o
α = 180−120 = 60o
ponieważ AO = DO = 9 i kąt α = 60o to ΔAOD jest równoboczy i AD = 9
z tw Pitagorasa:
AB = √BD2 − AD2 = √182 − 92 = √405 = 9√5
pole
P = AB*AD = 9*9√5 = 81√5 cm2
zad 2
AC = DB = 18
β = 120o
α + β = 180o
α = 180−120 = 60o
ponieważ AO = DO = 9 i kąt α = 60o to ΔAOD jest równoboczy i AD = 9
z tw Pitagorasa:
AB = √BD2 − AD2 = √182 − 92 = √405 = 9√5
pole
P = AB*AD = 9*9√5 = 81√5 cm2
 zad 3
a = 24 cm
β = 120o
2α + β = 180o suma kątów trójkąta
2α = 180−120 = 60o
α = 30o
zad 3
a = 24 cm
β = 120o
2α + β = 180o suma kątów trójkąta
2α = 180−120 = 60o
α = 30o
 zad 4
zad 4
 zad 5
dane
a = 21 cm
b = 12 cm
c = 15 cm
x = a−b = 9
z tw Pitagorasa
h = √c2 − x2 = 12
d = h = 12 cm
z tw Pitagorasa
e = √a2 + d2 = √585 = 3√65
f = √b2 + d2 = √288 = 12√2
zad 5
dane
a = 21 cm
b = 12 cm
c = 15 cm
x = a−b = 9
z tw Pitagorasa
h = √c2 − x2 = 12
d = h = 12 cm
z tw Pitagorasa
e = √a2 + d2 = √585 = 3√65
f = √b2 + d2 = √288 = 12√2

 a = 10√3
d = 15
d2 = a2+c2 − 2a*c*cos60o
c2 − 10√3c + 75 = 0
Δ = 0
c = 5√3
a = 10√3
d = 15
d2 = a2+c2 − 2a*c*cos60o
c2 − 10√3c + 75 = 0
Δ = 0
c = 5√3

 a = r + 12
b = r + 5
c = 5+12 = 17
a2 + b2 = 172
(r + 12)2 + (r + 5)2 = 289
po rozwiązaniu
r = 3
r = −20 → odrzucamy
a = 3 + 12 = 15
b = 3 + 5 = 8
a = r + 12
b = r + 5
c = 5+12 = 17
a2 + b2 = 172
(r + 12)2 + (r + 5)2 = 289
po rozwiązaniu
r = 3
r = −20 → odrzucamy
a = 3 + 12 = 15
b = 3 + 5 = 8

 d = 8
d = 8
 jakie są figury płaskie
jakie są figury płaskie