JAK TO ZROBIĆ??? Mietek: dany jest trapez ABCD o podstawie AB mającej długość 12.Na podstawie CD obrano punkt P taki że DP=4 odcinek BP przecina przekątną AC w punkcie R.Pole trójkąta ABR jest równe polu czworokąta ARPD. Oblicz długość odcinka PC.

Mietek: Panowie i Panie proszę o pomocD:

Mietek: ?

Mietek:

Mietek: ?

Mietek: ?

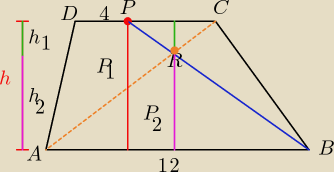
Eta: pola P₁=P₂ z treści zadania h₁+h₂= h ( trapezu ABCD)

	4+12
Pole trapezu ABPD =2P(ΔABR)=		*h = 8 h
	2

	1
P2= P(ΔABR)=		*12*h2= 6h2
	2

to 6h₂= 8h

	2
h2=		h
	3

	1
to: h1=		h
	3

z podobieństwa trójkątów ΔABR ~ΔPCR mamy:

	|PC|		h1		1
		=		=
	|AB|		h2		2

to: |PC|= 6

Eta: I co? ......... pasuje?

Mietek: dziękuje

WSP: hmm zastanawie mnie tylko dlaczego 6h2= 8h skoro Pole trapezu ABPD= 2P(ΔABR) powinno być raczej że 8h=2*6h2: