analityczna adam666: prosta y=−2x+2 przecina okrąg (x+3)² + (y+2)² = 25 w pkt A B. Wyznacz cosinus kąta ASB gdzie S jest środkiem okręgu. Proszę o szybką pomoc. Skąd wziąć A i B? mam amnezje...

think: rozwiązując układ równań:

⎧	y = −2x + 2
⎩	(x + 3)2 + (y + 2)2 = 25

metodą przez podstawienie daje równanie kwadratowe, w którym musisz policzyć pierwiastki i to będą pierwsze współrzędne tych punktów, drugie liczysz wstawiając do równania y = −2x + 2 (x + 3)² + (−2x + 2 + 2)² = 25 x₁ =....⇒ y₁ =.... x₂ =....⇒ y₂ =....

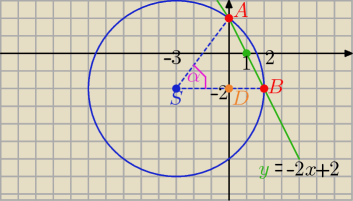
Eta: 1/ sposób algebraicznie S( −3, −2) r= 5 Rozwiąż układ równań y= −2x +2 (x+3)²+(y+2)²= 25 otrzymasz: A( 0,2) , B( 2, −2) |AB|= √20 i ze wzoru cosinusów dla ΔASB

	r2+r2−IABI2		3
cos(<ABS) =		=
	2r*r		5

2/ sposób graficznie: r= 5 |SD|= 3

	|SD|		3
cos(<ASB)=		=
	r		5