;/ Grześ1992: W trójkąt prostokątny o przyprostokątnych o długościach 2 i 4 wpisano prostokąt w ten sposób, że dwa jego boki leżą na przyprostokątnych trójkąta, a jeden z wierzchołków prostokąta leży na przeciwprostokątnej trójkąta. Prostokąt ten obraca się dookoła prostej, zawierającej dłuższą przyprostokątną trójkąta, tworząc walec. Oblicz, który z walców, otrzymanych w powyższy sposób, posiada największe pole powierzchni bocznej i oblicz jego objętość.

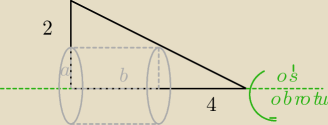
think: chodzi o maksymalizację pola powierzchni bocznej P_b = 2πab czyli można to uprościć do maksymalizacji pola prostokąta... P = a*b 0 < a < 2 0 < b < 4

a		4 − b		4 − b
	=		⇒ a =
2		4		2

	4 − b
P(b) =		*b → max policz współrzędne wierzchołka tej paraboli
	2