zestawy całek John: Proszę o sprawdzenie 1.całki nieoznaczone

	x4
a)∫(x3+cosx)dx = ∫ x3 dx + ∫cosx dx =		+sinx + c
	4

	1		1
b)∫(√x+		)dx = ∫x12 + ∫		dx = U{x32{32} + lnx =
	x		x

	2
		x32+ lnx + c
	3

	1		1		2x
c)∫(ex + 2x +		)dx = ∫ex dx + ∫2x dx + ∫		dx = ex +		+ tgx
	cos2x		cos2x		ln2

+ c 2)przez podstawienie

	t10		(2+x)10
a)∫(2+x)9 dx = | 2+x = t; dx=dt | = ∫ t9 dx =		+c =		+ c
	10		10

	t52
b) ∫x√x−2 dx = |x−2 =t; dt = dx; x = t+2 | = ∫(t+2)√t * dt =		+
	52

	t32		2		4
2		+ c =		t2√t+		t√t+c =
	32		5		3

	2		4
		(2+x)2(√2+x)+		(2+x)(√2+x)+c
	5		3

jo: Dobrze

john: jak zrobić to: oblicz objętość bryły otrzymanej przez obrót dokoła osi Ox trapezu krzywoliniowego ograniczonego hiperbolą xy=4, prostymi x=3, x=5 i y=0

Godzio:

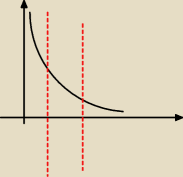
	4
V = π * 53∫(		)2dx
	x

john: nie czaje

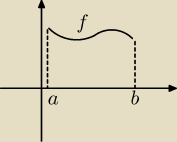Godzio: Jeśli liczymy objętość jakieś bryły powstałem przez obrót pewnej funkcji wokół osi OX na odcinku [a,b] to wzór jest taki: V = π * ^b_a∫f²(x)dx

john: aha

	x−1		1		1		1
v=16π 53 ∫ x−2 dx = 16π [		]= −16π[		]= 16π(		−		)= −
	−1		x		5		3

	2		32
16π(−		) =		π
	15		15

john: oblicz pole obszaru zawarte miedzy liniami y =x² i y=x+2 |D| = ²₋1 ∫ (y+2 − x²) dx

john:

john: ∫ od e do 1 x ln x dx = U=lnx U' = x

	1		x2
V'=		v=
	x		2

	lnx		x2		lnx		1		lnx
= x2 *		− ∫		x dx = x2 *		−		∫ x dx = x2 *		−
	2		2		2		2		2

	x2
		+ c =
	2

	x2		e2		1
[		*(lnx−1)]e1 + c =		*(lne−1)−		*(ln1−1)+c
	2		2		2

pjo: całka (3*2^x−2*3^x)/2^x, pomocy głowa pęka