podpis.:
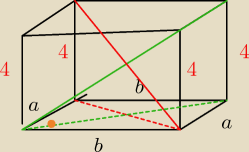
zaczynamy od rysunku.
DANE:
2a + 2b = 18
przekątna krótsza (czerwona) =
√33
przekątna dłuższa (zielona) = 9
h = 4
SZUKANE:
V = ?
żeby obliczyć V = P
p*H musimy znać pole podstawy, bo wysokość już mamy. Czyli potrzebujemy
tylko Pola podstawy.
nazwijmy tak:
C − przekątna krótsza (czerwona) =
√33
Z − przekątna dłuższa (zielona) = 9
c − przekątna podstrawy któtsza (czerwona przerywana)
z − przekątna podstawy dłuższa (zielona przerywana
H − wysokość = 4
obliczmy pierwsze −−−>c oraz z
−−−−>liczymy c z twierdzenia pitagorasa
H
2 + c
2 = C
2
c
2 = 33 − 16 = 17
c =
√17
−−−−−> liczymy z z twierdzenia Pitagorasa
Z
2 = z
2 + H
2
z
2 = Z
2 − H
2
z
2 = 81 − 16 = 65
z =
√65
no i mamy przekatne podstawy.
Teraz jest taki wzór na to aby mając przekątne policzyć a i b.
z
2 + c
2 =2*(a
2 + b
2)
65+17 = 2*(a
2 + b
2)
82 = 2*(a
2 + b
2) / dzielone na 2
41 = a
2 + b
2
i mamy jeszcze założenie
2a + 2b = 18 => a = 9−b
podkładamy
41 = 81 − 18b + b
2 + b
2
2b
2 −18b + 40 = 0
b
2 − 18b + 20 = 0
Δ = 324 − 80 = 244
√Δ = 2
√61
b
1 =
18 − 2√612 = 9 −
√61
b
2 =
18 + 2√612 = 9 +
√61
wtedy
a
1 =
√61
a
2 = −
√61
widać ze przypadek drugi nie może być bo a
2 jest mniejsze od 0 a długość boku musi być
przecież dodatnia. czyli mamy
a =
√61
b = 9 −
√61
sprawdźmy czy się zgadza
2*
√61 + 2*(9−
√61) = 18
zgadza się
ale mamy narazie tylko a i b a trzeba nam pole podstawy.
gdzieś się chyba pomyliłem kto znajdzie błąd.
