Rozwiąż nierówność
bil: | x3+x2+x | |
| > lub równe 0 |
| 9x2−25 | |
17 mar 22:41
Eta:
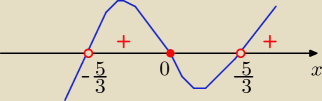
rozkładamy licznik i mianownik na czynniki
licznik: x( x
2+x+1) , Δ<0 , czyli wyrazenie x
2+x+1 jest dodatnie
mianownik: ( 3x−5)(3x+5)
| | 5 | | 5 | |
dziedzina: D= R \ { − |
| , |
| }
|
| | 3 | | 3 | |
zamieniamy teraz do postaci iloczynu:
x( 3x−5)(3x+5)( x
2+x+1) ≥0 , ponieważ wyrażenie x
2+x+1 >0
to: x( 3x−5)(3x+5) ≥0
| | 5 | | 5 | |
miejsca zerowe: x= 0 lub x= − |
| lub x= |
|
|
| | 3 | | 3 | |
uwzględniając dziedzinę mamy:
| | 5 | | 5 | |
odp: x€ ( − |
| ,0> U ( |
| , ∞)
|
| | 3 | | 3 | |
17 mar 22:57
bil: no tak... dzięki
17 mar 23:02
Eta:
17 mar 23:03
bil: no tak... dzięki
17 mar 23:07
ceaser I: Eta, dlaczego zakładasz że w liczniku Δ<0?
17 mar 23:21
Godzio:
Eta tego nie zakłada, to jest stwierdzenie
17 mar 23:23
ceaser I: a dobra już wiem, chodzi o to że parabola i tak ma ramiona do góry, jak nie ma miejsc 0 to x∊R,
tak ?
17 mar 23:25
Godzio: tak
17 mar 23:26
Eta:
Dokładnie tak
17 mar 23:28
Eta:
Dla
Godzia 
17 mar 23:29
Godzio :
Codziennie tyle jabłek dostaje, że już nie mam co z nimi robić
Tym razem się odwdzięczę:
i
żeby nie usnąć
17 mar 23:33
Eta:
18 mar 00:15