| k2+1 | ||
a) an= | n | |
| k |
 an = k2 + 1k * n = k2n + nk
teraz liczymy dla n+1
an+1 = k2 + 1k * (n+1) = k2n + k2 + n + 1k
teraz −−−> an+1 − an = k2n + k2 + n + 1k − (k2n + nk) = k2 + 1k
<−−− i to jest nasza różnica.
z godnie z tym co tutaj przeczytałem −−−> http://odpowiedz.pl/43481/43481/ciagi-2-przyklady-i-kiedy-rosnacy-a-malejacy.html
ciąg jest malejący gdy ta różnica jest niedodatnia, czyli ≤ 0
k2 + 1k ≤ 0
http://hajnowka.net/matematyka/row_nie_wymier.html
k≠0 <−−− założenie
(k2 + 1)(k) ≤ 0
k1 = 0
k2 + 1 = 0 => k2 = −1 => k∊∅
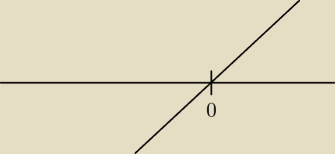
patrz rysunek.
k∊ (−∞, 0>, ale k≠0 więc k∊(−∞, 0)
Odp.: Dla k∊(−∞, 0) ciąg jest malejący
an = k2 + 1k * n = k2n + nk
teraz liczymy dla n+1
an+1 = k2 + 1k * (n+1) = k2n + k2 + n + 1k
teraz −−−> an+1 − an = k2n + k2 + n + 1k − (k2n + nk) = k2 + 1k
<−−− i to jest nasza różnica.
z godnie z tym co tutaj przeczytałem −−−> http://odpowiedz.pl/43481/43481/ciagi-2-przyklady-i-kiedy-rosnacy-a-malejacy.html
ciąg jest malejący gdy ta różnica jest niedodatnia, czyli ≤ 0
k2 + 1k ≤ 0
http://hajnowka.net/matematyka/row_nie_wymier.html
k≠0 <−−− założenie
(k2 + 1)(k) ≤ 0
k1 = 0
k2 + 1 = 0 => k2 = −1 => k∊∅
patrz rysunek.
k∊ (−∞, 0>, ale k≠0 więc k∊(−∞, 0)
Odp.: Dla k∊(−∞, 0) ciąg jest malejący
| k2+1 | ||
. Widać również, że licznik jest zawsze >0. Zatem znak całego ułamka zależy od | ||
| k |