trapez biedronka: krótsza podstawa trapezu jest równa wysokości tego trapezu i ma dlufość 12.Ramiona trapezu tworzą z dłuższą jego podstwą kąty o miarach 60 i 45 stopni.Oblicz pole i obwód.

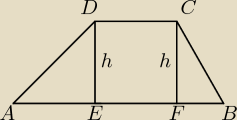
Dr Wykręt: h=|EF|=|CD|=12 kąt FBC=60⁰ ⇒ kąt BCF=30⁰ kąt EAD=kąt ADE=45⁰ 1) Obliczyć pole. 2) Obliczyć obw. 1) Możemy sobie podzielić nasz trapez na trzy figury: kwadrat (CDEF), trójkąt (BCF) i drugi trójkąt (ADE). Suma ich pól da pole całego trapezu. Z kwadratem nie ma problemu, jego pole wynosi h² (jego bok ma długość h), czyli 12²=144 Znamy długości boków trójkąta ADE, gdyż przyprostokątna |DE| jest równa |AE|, z uwagi na to, że jest to trójkąt prostokąty o kątach 45⁰, czyli jest równoramienny. Pole liczymy ze zwykłego

	1		1
wzoru na pole trójkąta, czyli P=		*|AE|*h=		*12*12=72
	2		2

Żeby obliczyć pole trójkąta BCF potrzebujemy długości |BF|, podstawy tego trójkąta (wysokość już mamy − h). Wiemy, że jest to trójkąt prostokątny o kątach 30 i 60 stopni. Wykorzystamy więc twierdzenie sinusów, które mówi, że dla dowolnego trójkąta, stosunek długości boku do sinusa przeciwległego kąta jest równy stosunkowi dowolnej innej długości boku do odpowiadającemu mu (przeciwległemu) sinusowi kąta. Na podstawie tego twierdzenia możemy ułożyć równanie:

	|FB|
U{h}{sin600)=
	sin300

Wyznaczamy |FB|, funkcje trygonometryczne zamieniamy na odpowiednie dla kąta wartości, i

	h√3
otrzymujemy: |FB|=		=4√3
	3

	1
Pole zatem wyniesie: P=		*|FB|*h=24√3
	2

Suma obliczonych pól daje nam pole trapezu: ∑P=144+72+24√3=216+24√3=24(9+√3) Innym sposobem jest użycie klasycznego wzoru na pole trapezu (możemy tak zrobić, gdyż wyliczyliśmy po drodze boki |AE| i |FB|, które wraz z bokiem |EF| dadzą nam |AB|, czyli całą dolną podstawę trapezu).

	1		1
P=		*h*(|CD|+|AB|)=		*12*(12+24+4√3)=216+24√3=24(9+√3)
	2		2

2) Liczymy obwód. Długość |AB| i |CD| mamy, czas zająć się ramionami. Ramię |AD| możemy obliczyć z użyciem funkcji trygonometrycznych, twierdzenia sinusów bądź tw pitagorasa. Ja tutaj użyję dla odmiany tego ostatniego. |AD|²=|AE|²+|DE|² |AD|²=144+144=288 |AD|=√288=12√2 Ramię |BC| liczymy z użyciem zależności trygonometrycznych:

|CF|		√3
	=cos300=		⇒ |BC|=8√3
|BC|		2

Obw=|AB|+|CD|+|AD|+|BC|=24+4√3+12+12√2+8√3=4(9+3√3+3√2)

biedronka: dzięki