okr ag i promień
dsf: Mam trójkąt równoramienny. Kąt między ramionami wynosi 2α. Długość podstawy to 10. Oblicz
promień okręgu wpisanego w ten trójkąt. JAKIEŚ POMYSLY ?

17 mar 14:27
dsf: wiem jak obliczyć promień okręgu opisanego na ale co dalej

17 mar 14:28
dsf: wiem, ze to jest pewnie proste ale serio nie rozumiem
17 mar 14:35
dsf: prosze o pomoc

17 mar 15:18
8: masz jakiś wynik do tego zadania
17 mar 15:59
dsf: właśnie niestety nie
17 mar 16:00
dsf: ?
17 mar 16:22
8: 10/2tg(45stopni−0,5α)=r
wynik mi tyle wyszło
17 mar 16:29
dsf: oj matko kochana a mogłabyś mi napisać jak to wyliczyłeś/as?
17 mar 16:42
7:
0
17 mar 16:54
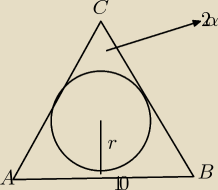
7: taki masz rysunek ? tten okrąg jest styczny do każdego boku ale mi cos nie wyszedł
17 mar 16:55
dsf: tak taki sam
17 mar 16:58
Dr Wykręt:
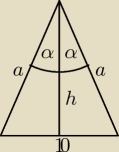
Promień okręgu wpisanego w ten trójkąt będzie wynosił:
Liczymy najpierw pole trójkąta P, do którego to potrzebujemy wysokości h. Korzystamy z
zależności trygonometrycznych.
Teraz liczymy a, również z zależności trygonometrycznych:
No i podstawiamy do wzoru początkowego na r:
| | 2P | | | | 50 | |
r= |
| = |
| =U{ |
| }{U{10+10sinα}{si |
| | a+a+10 | | | | taα | |
| | 50 | | sinα | |
nα}}= |
| * |
| |
| | tgα | | 10+10sinα | |
| | sinα | |
Biorąc pod uwagę, że tgα= |
| , możemy dojść do postaci: |
| | cosα | |
Niektóre obliczenia trochę na oko, ale powinno być dobrze. Pozdrawiam.
17 mar 17:10



 0
0
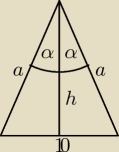 Promień okręgu wpisanego w ten trójkąt będzie wynosił:
Promień okręgu wpisanego w ten trójkąt będzie wynosił: