:)
M4ciek: W walec wpisano prostopadloscian. Przekatna tego prostopadloscianu tworzy z krawedziami jego
podstawy katy α i β.Oblicz stosunek objetosci prostopadloscianu do objetosci walca.
17 mar 13:31
17 mar 13:36
M4ciek: Poprosze o jakies sugestie bo jeszcze jakos V prostopadloscianu bym policzyl, ale walca to nie
mam pojecia...

Wpadne wieczorem , z gory dziekuje

17 mar 13:38
M4ciek: Podbijam

17 mar 18:39
M4ciek: W gore ^^
17 mar 18:53
M4ciek: Podbijam

17 mar 19:11
M4ciek: Podbijam...
17 mar 19:22
Godzio: hmmm

Momencik
17 mar 19:23
M4ciek: O [p{Godziu]] jestem uratowany

17 mar 19:28
M4ciek: Godziu*
17 mar 19:28
Godzio:
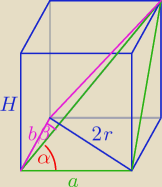
d − przekątna prostopadłościanu
a
2 + b
2 = (2r)
2 ⇒ r = ...
I dalej chyba już będzie łatwo, wysokości liczyć nie trzeba bo ona i tak się w liczeniu tego
stosunku skróci

17 mar 19:36
ICSP: Godziu podziękowałem ci za tamto zadanko ci mi kiedyś zrobiłeś?
17 mar 19:38
Godzio:
Nie pamiętam już nawet jakie

17 mar 19:41
ICSP: Ostatnie takie z ostrosłupem w którym wysokosc jest dwa razy większa trzeba obliczyć cosinus
miedzy sąsiednimi ścianami bocznymi

17 mar 19:42
Godzio:
Podziękowałeś

17 mar 19:43
M4ciek:
A skad sie to wzielo :
17 mar 19:47
Godzio: Przyrównałem d

17 mar 19:47
ICSP: Co prawda zrobiłem to w koncu w inny sposób bo nie dałem rady z tym układem równań:(
17 mar 19:53
M4ciek:
A teraz cos innego :
Wyznacz wspolrzedne punktu,bedacego srodkiem symetrii tego szesciokata.Uwzglednij dwa
przypadki.
Mam z wczesniejszego podpunktu wyliczony bok = 6, i podane dwa sasiednie wierzcholki A = (2,0)
i B = (5,3√3).
17 mar 19:55
Godzio:
Dobrze myślę że to z czerwonej książki te zadania, bo jakoś ostatnio je robiłem
17 mar 20:00
Godzio:
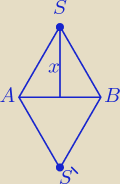
Mogę tak doradzić, może nie jest to najszybszy sposób ale zawsze

Wyznacz równanie prostej przechodzącej przez AB, a następnie wyznacz odległość punktu S(x,y) od
tej prostej i oblicz jego współrzędne wiedząc że ta odleglość jest równa x, ją sobie prosto
policzysz bo to wysokośc trójkąta równobocznego

17 mar 20:06
M4ciek:
Tak z czerwonej

Tez tak myslalem z tym , ale nie bylem pewien.
A wracajac do tego wczesniej to :
V
prostopadloscianu = a*b*H
I te boki zostawic po prostu zapisane jako a i b


17 mar 20:12
Godzio:
Tak, ale "a" jest wyrażone za pomocą "b", tak samo promień walca też jest wyrażony za pomocą
"b", H się skróci, b2 także więc zostaną same wartości liczbowe
17 mar 20:15
M4ciek: Zaraz napisze obliczenia dla sprawdzenia

17 mar 20:17
M4ciek:
a
2 + b
2 = (2r)
2
a
2 + b
2 = 4r
2
| | bcosα | |
( |
| )2 + b2 = 4r2 |
| | cosβ | |
| b2cos2α | | b2cos2β | |
| + |
| = 4r2 |
| cos2β | | cos2β | |
| b2(cos α + cos β) | |
| = 4r2 |
| cos2β | |
| b2(cos α + cos β) | |
| = r2 |
| 4cos2β | |
| | b√cos α + cos β | |
r = |
| |
| | 2cos β | |
V
walca = π*r
2*H
| | b2(cos α + cos β) | |
Vwalca = π* |
| *H |
| | 4cos2β | |
17 mar 20:28
Godzio:
Ok, tylko kwadraty Ci zniknęły: cos
2α + cos
2β

17 mar 20:31
M4ciek:
V
prostopadloscianu = a * b * H
| | bcosα | |
Vprostopadloscianu = b * |
| * H |
| | cosβ | |
| Vprostopadloscianu | | | |
| = |
| |
| Vwalca | | | πb2(cos α + cos β)*H | |
| | | 4cos2β | |
| |
Tak


| Vprostopadloscianu | | | |
| = |
| |
| Vwalca | | | |
| Vprostopadloscianu | | cos α | |
| = |
| |
| Vwalca | | | |
| Vprostopadloscianu | | 4cos α cos β | |
| = |
| |
| Vwalca | | π(cos α + cos β) | |
17 mar 20:39
Godzio:
Tylko te kwadraty i ok

17 mar 20:40
M4ciek:
Ok

Duzooo pisania

17 mar 20:41
Godzio: Czasem trzeba się namęczyć

17 mar 20:44
M4ciek: Jeszcze wpadne pozniej pomeczyc sie z ta symetria

Bedziesz


17 mar 20:51
Godzio:
Postaram się być

17 mar 20:55
M4ciek: Jestes jeszcze
Godziu 

17 mar 23:05
Godzio :
No czekam czekam cały czas

17 mar 23:06
M4ciek: Na tym Twoim rysunku to jest romb , a ja mam szesciokat chyba ,ze to jakis uproszczony rysunek

17 mar 23:07
Godzio :
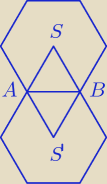
Teraz pasuje

?
17 mar 23:09
17 mar 23:11
M4ciek: Dobra licze , zaraz wkleje co mi tu wyszlo

17 mar 23:12
M4ciek:
A = (2,0) , B = (5,3
√3)
(5 − 2)(y − 0) = (3
√3 − 0)(x − 2)
3y = 3
√3x − 6
√3
y =
√3x − 2
√3
x = 3
√3 = d , −
√3x + y + 2
√3 = 0
| | IAxo + Byo + CI | |
d = |
| |
| | √A2 + B2 | |
| | −√3xo + yo + 2√3 | |
3√3 = |
| |
| | √(−√3)2 + 12 | |
6
√3 = −
√3x
o + y
o + 2
√3
4
√3 = −
√3x
o + y
o
I jak wyznaczyc te wspolrzedne


17 mar 23:24
Godzio:
Trzeba wyznaczyć równanie prostej prostopadłej przechodzącej przez środek AB i wtedy już
będziesz mógł to wyznaczyć

, i dlaczego zniknęła Ci wartość bezwzględna ?

17 mar 23:26
M4ciek: Yyy zgubilem ja

to bedzie
4
√3 =
√3x
o + y
o 

17 mar 23:28
Godzio :
To będzie:
6√3 = |−√3xo + yo + 2√3| i z tym narazie nic nie możesz robić, wyznacz równanie tej
prostej prostopadłej, punkt S(xo,yo) spełnia równanie tej prostej więc za yo możesz
podstawić to co wyliczysz
17 mar 23:31
M4ciek:
y =
√3x − 2
√3
| | 1 | | √3 | |
a1 * a2 = −1 ⇒ a2 = − |
| ⇒ − |
| |
| | √3 | | 3 | |
17 mar 23:34
Godzio :
Podstawić i z def. wart. bezwzględnej
17 mar 23:37
M4ciek:
| | √3 | | 8√3 | |
6√3 = I−√3x − |
| x + |
| + 2√3I |
| | 3 | | 3 | |
| | 4√3 | | 14√3 | |
6√3 = I− |
| x + |
| I |
| | 3 | | 3 | |
| | 4√3 | | 14√3 | | 4√3 | | 14√3 | |
− |
| x + |
| = 6√3 v − |
| x + |
| = −6√3 |
| | 3 | | 3 | | 3 | | 3 | |
x
1 = ... v x
2 = ...
x
1 i x
2 podstawic do :
17 mar 23:42
Godzio :
Tak
17 mar 23:46
M4ciek: Uff

Dziekuje bardzo za pomoc

A jak przygotowania do matury

17 mar 23:47
Godzio :
Idą powoli zwłaszcza z przedmiotów ≠ matematyki

17 mar 23:48
M4ciek: Bo Ty zdajesz niemiecki i fizyka R


17 mar 23:53
Godzio:
Tak jest

17 mar 23:54
M4ciek: Jak Fizyka leci bo to chyba najgorsze dla Ciebie


17 mar 23:57
Godzio:
Z fizyki jakoś jeszcze idzie, ja się zastanawiam co ja powiem na niemieckim ustnym rozszerzonym

17 mar 23:59
think: Guten Morgen [czyt. butem w mordę]

18 mar 00:01
Godzio: think tutaj utalentowana językowo widzę

18 mar 00:02
M4ciek: 
Rozszerzony niemiecki

18 mar 00:06
M4ciek: Hej
think 
18 mar 00:06
think: no baaa

18 mar 00:07
think: hej
M4ciek witaj
Godzio
właściwie to dobranoc, co prawda nie chce mi się spać tak jak chce mi się rano, ale trzeba
zacząć normalniej funkcjonować, bo obawiam się, że mój szef straci w końcu do mnie cierpliwość

jak to dobrze, że przy okazji jestem jedyną i ulubioną córką tego szefa

18 mar 00:08
think: M4ciek widzę, że wałkujesz zadanka ze stereometrii

możliwe, że Cię to rozbawi... ale obawiam
się, że najlepiej je zrozumiesz i będziesz umiał sobie wszystko wyobrazić po maturze

na
maturze może być różnie a po to się okaże nagle takie łatwe, proste i nieskomplikowane

18 mar 00:11
M4ciek: 
ja moge pospac jutro bo mam rekolekcje

18 mar 00:11
Godzio:
Ja chyba niedługo zacznę brać tabletki na sen, bo inaczej nie zaczne chodzić spać o normalnej
godzinie ...
18 mar 00:11
M4ciek: Zobaczymy co to bedzie

Mam probna podstawe w szkole w poniedzialek

18 mar 00:12
Godzio:
Też bym mógł

tyle że jutro pierwsze 2 matmy więc opuścić nie można

18 mar 00:12
lalalalala: człowieku po co ty jeszcze na matme chodzisz skoro i tak wszystko ogarniasz xd
18 mar 00:13
think: kwestia przyzwyczajenia, lepiej nie bierz tabletek, bo jak się do nich przyzwyczaisz to później
się okaże, że nie ważne która godzina to nie możesz spać bez nich. Kilka dnia z rzędu wstań o
świcie to i zetnie Cię o przyzwoitej porze do łóżka

18 mar 00:14
M4ciek: Wlasnie
Godziu po co Ty chodzisz jeszcze na mate

mnie to zawsze zastanawia


18 mar 00:18
think: dobra ja zmykam

Jakoś ostatnio nie dzieje się nic, co by jakoś strasznie przykuło moją uwagę, też
zauważyliście, że brak wyzwań w tych zadaniach ? ? ?

znowu rutyna.
18 mar 00:18
M4ciek:
Think Ty juz zrobilas tyle zadan ,ze wiekszosc dla Ciebie to rutyna

Dobranoc

18 mar 00:20
Godzio :
Chodzę, bo to jeden z 3 przedmiotów na których się nie nudzę, zawsze jest coś do roboty.
18 mar 00:20
Godzio : Dobranoc


18 mar 00:21
think: M4ciek mhm, na ogół to rutyna póki odpowiedzi się zgadzają

a jak się nie zgadzają to jest
jazda

18 mar 00:22
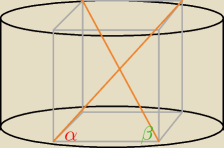
hahnne: Nie wiem, czy ktoś jeszcze odpowie w tak zawiłym wątku, ale nie zaszkodzi spróbować

Ja odnośnie zadania, które rozwiązał wyżej M4ciek, tego z prostopadłościanem wpisanym w walec.
Jest taki fragment rozwiązania, którego nie potrafię zrozumieć. Chodzi o post z 17 marca z
20:28
Kiedy M4ciek liczy z Pitagorasa: a
2+b
2=4r
2
i ma postać:
| | bcosα | |
( |
| )2 + b2 = 4r2 |
| | cosβ | |
i w następnej linijce za b podstawia:
Czy b to nie czasem:
28 kwi 20:06
 Tak to bedzie wygladalo
Tak to bedzie wygladalo 

 Wpadne wieczorem , z gory dziekuje
Wpadne wieczorem , z gory dziekuje 


 Momencik
Momencik

 d − przekątna prostopadłościanu
d − przekątna prostopadłościanu







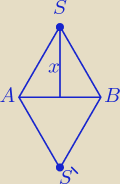
 Wyznacz równanie prostej przechodzącej przez AB, a następnie wyznacz odległość punktu S(x,y) od
tej prostej i oblicz jego współrzędne wiedząc że ta odleglość jest równa x, ją sobie prosto
policzysz bo to wysokośc trójkąta równobocznego
Wyznacz równanie prostej przechodzącej przez AB, a następnie wyznacz odległość punktu S(x,y) od
tej prostej i oblicz jego współrzędne wiedząc że ta odleglość jest równa x, ją sobie prosto
policzysz bo to wysokośc trójkąta równobocznego 
 Tez tak myslalem z tym , ale nie bylem pewien.
A wracajac do tego wczesniej to :
Vprostopadloscianu = a*b*H
I te boki zostawic po prostu zapisane jako a i b
Tez tak myslalem z tym , ale nie bylem pewien.
A wracajac do tego wczesniej to :
Vprostopadloscianu = a*b*H
I te boki zostawic po prostu zapisane jako a i b 






 Duzooo pisania
Duzooo pisania 

 Bedziesz
Bedziesz 






 Teraz pasuje
Teraz pasuje  ?
?







 , i dlaczego zniknęła Ci wartość bezwzględna ?
, i dlaczego zniknęła Ci wartość bezwzględna ? 
 to bedzie
4√3 = √3xo + yo
to bedzie
4√3 = √3xo + yo 



 Dziekuje bardzo za pomoc
Dziekuje bardzo za pomoc  A jak przygotowania do matury
A jak przygotowania do matury









 Rozszerzony niemiecki
Rozszerzony niemiecki 


 jak to dobrze, że przy okazji jestem jedyną i ulubioną córką tego szefa
jak to dobrze, że przy okazji jestem jedyną i ulubioną córką tego szefa 
 możliwe, że Cię to rozbawi... ale obawiam
się, że najlepiej je zrozumiesz i będziesz umiał sobie wszystko wyobrazić po maturze
możliwe, że Cię to rozbawi... ale obawiam
się, że najlepiej je zrozumiesz i będziesz umiał sobie wszystko wyobrazić po maturze  na
maturze może być różnie a po to się okaże nagle takie łatwe, proste i nieskomplikowane
na
maturze może być różnie a po to się okaże nagle takie łatwe, proste i nieskomplikowane 
 ja moge pospac jutro bo mam rekolekcje
ja moge pospac jutro bo mam rekolekcje 
 Mam probna podstawe w szkole w poniedzialek
Mam probna podstawe w szkole w poniedzialek 
 tyle że jutro pierwsze 2 matmy więc opuścić nie można
tyle że jutro pierwsze 2 matmy więc opuścić nie można 

 mnie to zawsze zastanawia
mnie to zawsze zastanawia 

 Jakoś ostatnio nie dzieje się nic, co by jakoś strasznie przykuło moją uwagę, też
zauważyliście, że brak wyzwań w tych zadaniach ? ? ?
Jakoś ostatnio nie dzieje się nic, co by jakoś strasznie przykuło moją uwagę, też
zauważyliście, że brak wyzwań w tych zadaniach ? ? ?  znowu rutyna.
znowu rutyna.
 Dobranoc
Dobranoc 


 a jak się nie zgadzają to jest
jazda
a jak się nie zgadzają to jest
jazda 
 Ja odnośnie zadania, które rozwiązał wyżej M4ciek, tego z prostopadłościanem wpisanym w walec.
Jest taki fragment rozwiązania, którego nie potrafię zrozumieć. Chodzi o post z 17 marca z
20:28
Kiedy M4ciek liczy z Pitagorasa: a2+b2=4r2
i ma postać:
Ja odnośnie zadania, które rozwiązał wyżej M4ciek, tego z prostopadłościanem wpisanym w walec.
Jest taki fragment rozwiązania, którego nie potrafię zrozumieć. Chodzi o post z 17 marca z
20:28
Kiedy M4ciek liczy z Pitagorasa: a2+b2=4r2
i ma postać: