Hej. :)
Igaa: Hej. Może mi ktoś narysować lub chociaż dać wskazówki jak narysować wykres funkcji
y = [ sinx ]
Bardzo proszę.
15 mar 19:33
Basia:
to jest entier czy wartość bezwzględna ?
15 mar 19:34
Igaa: to jest cecha z sin x
15 mar 19:37
Basia:
czyli entier, czyli część całkowita
ta funkcja przyjmuje wartości:
1 dla każdego x=π2+2kπ
0 w przedziałach <2kπ, π2+2kπ)∪(π2+2kπ, (2k+1)π>
−1 w przedziałach ( (2k−1)π, 2kπ)
15 mar 19:44
Igaa: ta... Nie mam pojęcia jak to narysować
| | π | |
Wgl to dlaczego jest x jest równe |
| + 3kπ |
| | 2 | |
15 mar 19:47
Igaa: | | π | |
Nie sory x = |
| + 2kπ |
| | 2 | |
15 mar 19:48
Basia:
bo dla x = π2+2kπ sinx = 1 ⇒ [sinx]=1
to będą punkty: (π2, 1) (5π2, 1) (9π2, 1) czyli te same, dla których sam
sinx=1
tam gdzie sinx≥0 i sinx≠1 masz 0
tam gdzie sinx<0 masz −1
15 mar 19:52
Igaa:
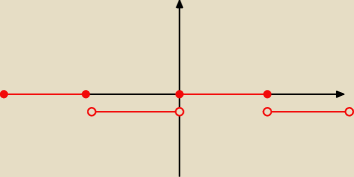
To tak będzie wyglądał wykres
15 mar 20:01
Igaa: | | x + 3 | |
A wiesz może jak narysować taki wykres? y = |
| |
| | x − 1 | |
15 mar 20:02
Basia:
| | x−1+4 | | x−1 | | 4 | | 4 | |
y = |
| = |
| + |
| = |
| +1 |
| | x−1 | | x−1 | | x−1 | | x−1 | |
| | 4 | |
rysujesz hiperbolę y = |
| i przesuwasz ją o wektor [1,1] |
| | x | |
15 mar 20:05
Igaa: OK. A taki y ≤ − x
2 + 1
15 mar 20:08
Basia:
to jest parabola y= −x2+1 [ramiona w dół, m.zerowe ±1, wierzchołek (0,1)] i wszystko co leży
poniżej czyli "między" jej ramionami
15 mar 20:11
Igaa: OK Dziękuje.
| | 4 | |
A jak rozpisać taką funkcje: y ≤ I |
| − 2 I |
| | IxI − 3 | |
15 mar 20:20
marcin: Czy ten wykres entier[sinx] powyzej jest na 100% prawidłowy
20 lis 20:19