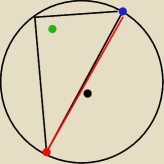
 Promień okregu jest rowny 4√2. oblicz dlugosc cieciwy AB.
Zielonym kolorem oznaczylem podany kat alfa = 105stopni
kolorem czerwonym oznaczylem cieciwe AB.
Promień okregu jest rowny 4√2. oblicz dlugosc cieciwy AB.
Zielonym kolorem oznaczylem podany kat alfa = 105stopni
kolorem czerwonym oznaczylem cieciwe AB.
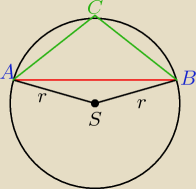 ∡ACB i ∡ ASB oparte są na tej samej cięciwie, więc kąt ∡ASB jest dwa razy większy od tego
drugiego − twierdzenie o kącie wpisanym i środkowym opartych na tej samej cięciwie.
Korzystając z twierdzenia cosinusów (w trójkącie równoramiennym ASB) obliczasz AB
|AB|2 = r2 + r2 − 2r2*cos 210
cos 210 można sobie zamienić na ładny kąt ze wzorów redukcyjnych cos (180 + 30)
∡ACB i ∡ ASB oparte są na tej samej cięciwie, więc kąt ∡ASB jest dwa razy większy od tego
drugiego − twierdzenie o kącie wpisanym i środkowym opartych na tej samej cięciwie.
Korzystając z twierdzenia cosinusów (w trójkącie równoramiennym ASB) obliczasz AB
|AB|2 = r2 + r2 − 2r2*cos 210
cos 210 można sobie zamienić na ładny kąt ze wzorów redukcyjnych cos (180 + 30)

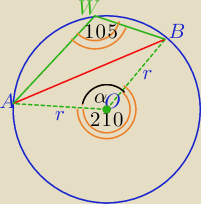 α=360−210=150
r=4√2
W ΔABO:
|AB|2=(4√2)2+(4√2)2−2*4√2*4√2*cos(150o)
|AB|2=64−64 (−cos30o)
α=360−210=150
r=4√2
W ΔABO:
|AB|2=(4√2)2+(4√2)2−2*4√2*4√2*cos(150o)
|AB|2=64−64 (−cos30o)
| √3 | ||
|AB|2=64+64* | =16*(4+2√3)=16*(1+√3)2 | |
| 2 |
| √6+√2 | ||
|AB|=8√2* | ||
| 4 |

