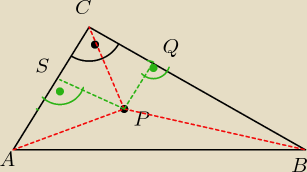
Planimetria Pomocy !: Poproszę o podpowiedź jakąś... W trójkącie prostojątnym ABC, |kat C|=90^o , wybrano punkt P, dla ktorego trojkaty PAB, PBC, PCA maja rowne pola. Widziac dodatkowe, ze |PA|² + |PB|²=45 oblicz dlugosc |PC|. Prosze nie rozwiązywać zadania, a jedynie nakierować mnie na właściwy trop, bo nie umeim go ruszyć..

Pomocy !:

Pomocy !: Proszę o jakąś wskazówkę

Godzio : Pomogę

Pomocy !: Cieszę się bardzo

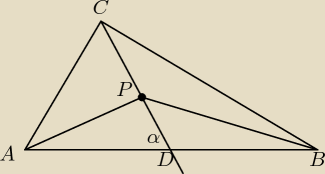
Godzio : Skoro wszystkie pola są równe, tzn. że są to środkowe trójkąta ABC, a one dzielą się w stosunku 2 : 1 więc można oznaczyć:

	2		1
|PC| =		x, |PD| =		x gdzie x = |CD|
	3		3

i skorzystać z tw. cosinusów w trójkącie ADP i PDB, pamiętaj, że cos(180 − α) = −cosα więc coś się skróci

Pomocy !: okej, zabieram się do pracy Dam znać

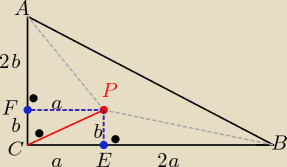
Eta: Można też tak: ponieważ pola trójkatów PAB, PBC, PAC sa równe

	1
to pole każdego z nich jest równe		P(ΔABC)
	3

zatem rzuty prostokątne E i F punktu P na przyprostokatne dzielą te przyprostokątne w stosunku 1: 2 licząc od wierzchołka C teraz z tw. Pitagorasa w trójkątach: PCF, PBE i PCE napisz zależności i uwzględnij,że |PC|²+ |PA|²= 45

Pomocy !: Eta, a skąd wiesz, że |CP|²+|CA|²=45 ?

Pomocy !: Przepraszam, |PC|² +|PA|² =45 *

Eta: oczywiście chochlik ma być |PA|²+ |PB|²= 45 , z treści zadania

Pomocy !: ok, rozumiem

Zeniciak: Jak robię to zadanie sposobem Godzia, to nie skraca mi się wynik. Robię tak: x = |PD| |PA|² = x² + |DA|² − 2|DA|*x*cosα |PB|² = x² +|DA|² − 2|DA|*x*(−cosα) |PA|² + |PB|² = 45 x² + |DA|² − 2|DA|*x*cosα + x² + |DA|² + |DA|*x*cosα = 45 czyli 2x² + 2|DA|² = 45 Pomocy

123qwe: Zeniciak zastosuj Δ