?? .aga: wykaż że prots l: y=−2x−1 jest styczna do okregu (x−3)²+(y+2)²=5

Bizon: ... sprawdż odległość środka tego okręgu od prostej ... czy czasami nie jest równa promieniowi

Bizon: albo układ równań .... więc (x−3)²+(−2x−1+2)²=5 ... i sprawdź czy czasami Δ nie jest równa 0. Jeśli tak to jest jedno rozwiązanie .... a więc jeden wspólny punkt ...

.aga: dzięki

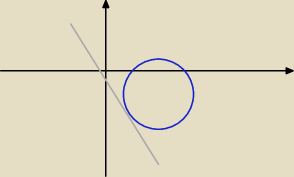
Licealistka: rysunek prowizorka: prosta może mieć z okręgiem jeden lub dwa lub zero punktów wspólnych. prosta jest styczna do okręgu jeżeli ma z nim dokładnie jeden punkt wspólny. Wyznaczanie punktów wspólne okręgu i prostej: (x−3)²+(−2x−1+2)²=5 x² −6x +9 +(−2x+1)² =5 x2 −6x +9 +4x² −4x +1 =5 5x² −10x +5=0 /:5 x² −2x +1=0 (x−1)²=0 ma punkt spólny (1;−3)