stozek w kuli gregi: W kule o objętosci V wpisano stożek, którego przekrój osiowy ma przywierzchołku kąt o mierze α. oblicz objetosc stozka

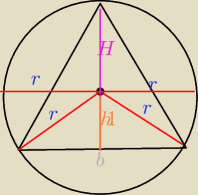
gregi: h1=a√3/2 h1=r√3/2 z Pitagorasa wynika ze b²=r²−(r√3/2)² b=r/2 dobrze i co dalej?

gregi: Pp= πr² Pp=(r/4)²π Pp=r²/16π H=r+h1 H=r+ r√3/2 V=1/3 πr²H V=1/3 r²* r+ r√3/2 dobrze? prosze o sprawdzenie mnie

kamis:

	a√3
Nie wiem skąd Ci się wzięło		, nie jest powiedziane czy przekrojem osiowym stożka
	2

jest trójkąt równoboczny, równie dobrze może nim być trójkąt równoramienny Objętość kuli: V = 4πR³

	V
R = 3√
	4π

Z twierdzenia sinusów:

b
	= 2R
sinα

b = 2Rsinα

b
	= Rsinα
2

h₁² = R²(1 − sin²α) h₁ = R√1 − sin²α ⇒ √1 − sin²α = cosα h₁ = Rcosα

	πR2sin2α
Objętość stożka:		* R(1 + cosα)
	3

gregi: dzieki

Ajtek: V kuli=⁴₃πR³

gregi: to jak to ma byc poprawnie?

gregi: no prosze piknie

gregi: na prawde pilne