Patter: Wyznacz zbiór roziązań równania |x+1|+|x−2|=p, w zależności od parametru p (p∊R)

Patter: Prosze o pomoc

Patter: Wiem, że mam to rozwiązać w trzech przedziałach na początek ? Tak ? A co dalej ?

Godzio : Narysuj wykres |x + 1| + |x − 2| w przedziałach i sprawdź w jakich przedziałach proste p przecinają wykres funkcji i ile razy − to będzie ten zbiór rozwiązań

Patter: ale nie umiem narysować wykresu takiej funkcji

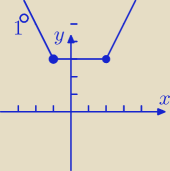
Godzio : Jeśli umiesz rozpatrzyć przypadki to i narysować byś umiał 1^o x ∊ (−∞,−1) f(x) = − x − 1 − x + 2 = −2x + 1 2^o x ∊ <−1,2) f(x) = x + 1 − x + 2 = 3 3^o x ∊ <2,∞) f(x) = 2x − 1 p ∊ (3,∞) −− 2 rozwiązania p ∊ (−∞,3) −− 0 rozwiązań p = 3 ⇒ nieskończenie wiele rozwiązań

Patter: yhy... Ale ja głupi jestem Nie pomyślałem, że to można tak zrobić ja to również liczyłem tyle że ty to zrobiłeś jako f(x)= a ja jako |x+1|+|x−2| = p i tu był mój błąd. nie powinienem tego do p przyrównywać. Mam rację ?

Godzio : To przyrównanie raczej nic by nie dało

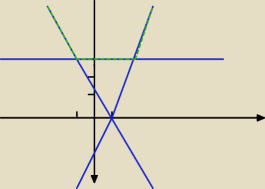Patter: Wg mnie wykres powinien wygladac mniej więcej tak. Dlaczego u ciebie jest tylko to co zaznaczyłem na zielono ? Przeież na dole też są jakieś rozwiązania, np. dla x∊(−∞0) − 2 rozwiazania dla x∊ {0} − 1 rozwiazanie dla x∊ (0,3) − dwa rozwiazania dla x∊ {3} − nieskonczenie wiele rozwiazań dla x∊ (3,+∞) − dwa rozwiazania

Godzio : Bo ty nie narysowałeś wykresu w przedziałach które rozpatrujesz, a tylko w nich możesz działać

Patter: A weź, żałosne było to pytanie Gdzie ja mam głowę ? Jeszcze jedno, bo w odpowiedziach mam tak :

	1+p		1−p
dla p∊(3,+∞) rozwiązaniem jest zbiór : {		,		} , możesz mi wyjaśnić dlaczego
	2		2

jest taki zapis ?

Godzio : W tym przedziale funkcja składa się z 2 wykresów: f(x) = −2x + 1 i f(x) = 2x − 1 Jak przyrównasz to do p to otrzymasz to co on chcą

	1 − p
p = −2x + 1 ⇒ x =
	2

	p + 1
p = 2x − 1 ⇒ x =
	2

Patter: Okej, rozumiem. Dziękuję Ci bardzo dobry człowieku