Pole
Kasienka: Drut o długości 120 cm chcemy wygiąć w prostokątną ramkę. Oblicz jakie wymiary powinna mieć ta
ramka, aby prostokąt, który ogranicza miał największe pole
12 mar 14:59
morfepl: 2x+2y=120cm
x+y=60cm
y=60cm−x
P=x(60cm−x)
P=−x2+60x
i teraz policz wierzchołek paraboli, ja nigdy nie pamiętam tego wzoru więc jadę pochodną
−2x+60=0
2x=60
x=30
12 mar 15:05
Vizer:
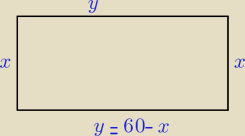
2x+2y=120
2y=120−2x
y=60−x
P=(60−x)x
P(x)=−x
2+60x
Parabola ma ramiona skierowane w dół więc wierzcholek paraboli osiąga najwieksza wartosc dla
funkcji
x
w=30
P=(60−30)*30
P=30*30=900[cm
2]
12 mar 15:08
Vizer: eh rozpedzielm sie i pole wyliczylem rzecz jasna wymiary powinny byc 30x30 czyli jest to
kwadrat
12 mar 15:09
Kasienka: dziękuję

12 mar 15:14
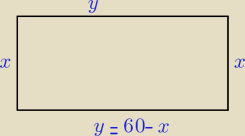 2x+2y=120
2y=120−2x
y=60−x
P=(60−x)x
P(x)=−x2+60x
Parabola ma ramiona skierowane w dół więc wierzcholek paraboli osiąga najwieksza wartosc dla
funkcji
2x+2y=120
2y=120−2x
y=60−x
P=(60−x)x
P(x)=−x2+60x
Parabola ma ramiona skierowane w dół więc wierzcholek paraboli osiąga najwieksza wartosc dla
funkcji
