planimetria
sk: W trapezie równoramiennym ABCD podstawa AB jest trzy razy dłuższa niż podstawa AB jset trzy
razy dłuższa niż podstawa CD. Udowodnij, że przekątne AC i DB trapezu dzielą odcinek KN
łączący środki jego ramion w stosunku 1:2:1.
12 mar 14:48
sk: odświeżam
12 mar 20:51
sk:
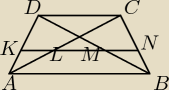
rysunek..
wiem, że trzeba to z Talesa i |KL|=1/2 |DC|
12 mar 22:13
sk: re
13 mar 17:34
Eta:
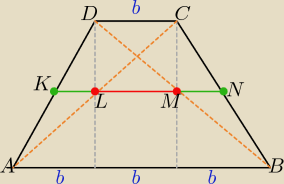
|AB|= 3b
Z tw. Talesa w trójkątach ACD i BCD
| | 1 | | 1 | |
|KL| = |
| b i |MN| = |
| b
|
| | 2 | | 2 | |
| | a+b | | 4b | |
długość środkowej trapezu: |KN|= |
| = |
| = 2b
|
| | 2 | | 2 | |
[C[|LM|] = |KN| − ( |KL| + |MN|) = 2b − b = b
zatem: |KL| : |LM| : |MN| =
12b : b :
12b= 1: 2 :1
c.n.u
13 mar 21:19
sk: dzięki
14 mar 13:42
feuu: "Z tw. Talesa w trójkątach ACD i BCD" moze mi to ktos w skrocie wytlumaczyc ?
19 mar 22:26
feuu: juz kumam =d
19 mar 23:27
mati: Z tw. Talesa w trójkątach ACD i BCD" moze mi to ktos w skrocie wytlumaczyc ?
bo ja nie czaje
7 kwi 20:54