zestaw rozszerzony Ewelina: w zależności od wartości parametru a ∊ R ułóż w kolejności rosnącej liczby: x=a, y=^a_a−1, z=a²−2a+2

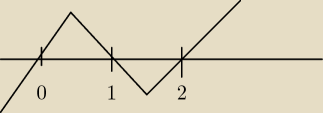
:P: a<^a_a−1 ^{a2 − a}_a−1 − ^a_a−1 < 0 ^{a2 − 2a}_a−1 < 0 (a² − 2a) * (a−1) < 0 a=1 a=2 a=0 x∊ (−∞, 0) ∪ (1,2) i do tego jeszcze musi być ^a_a−1 < a² − 2a + 2 ^a_a−1 < ^{a2 − 2a + 2}_a−1 * (a−1) ^a_a−1 < ^{a3 − 2a2 + 2a − a2 + 2a −2}_a−1 ^a_a−1 < ^{a3 − 3a2 + 4a −2}_a−1 ^a_a−1 − (^{a3 − 3a2 + 4a −2}_a−1) < 0 ^{−a3 + 3a2 − 3a + 2}_a−1 < 0 (−a³ + 3a² − 3a + 2) (a−1) < 0 a = 1 −a³ + 3a² − 3a + 2 = 0 x = 2, wtedy −8 + 12 −6 +2 = 0 schemat Hornera −1 +3 −3 +2 −2 2 −2 −1 1 −1 == −x² + x − 1 = 0 Δ = 1−4<0 nie ma więcej miejsc zerowych.czyli (−a³ + 3a² − 3a + 2) (a−1) < 0 a = 1 a = 2 rysunek niżej

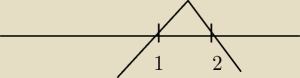
:P: a∊ (−∞, 1) ∪ (2, +∞) i teraz żeby było spełnione a < ^a_a−1 < a² − 2a + 2 to wtedy i tylko wtedy gdy −−−> a∊ (−∞, 0) ∪ (1, 2) ∩ a∊ (−∞, 1) ∪ (2, +∞) , czyli część wspólna a∊ (−∞, 0), czyli dla a∊ (−∞, 0) −−−> a < ^a_a−1 < a² − 2a + 2

:P: i teraz analogicznie trzeba rozpatrzyć warunek a > ^a_a−1 > a² −2a + 2 czyli najpierw −−−>a > ^a_a−1 i potem −−−−−> ^a_a−1 > a² −2a + 2 i część wspólną tych wyników. i to będą dopiero 2 możliwości później są jeszcze 4 możliwości: a > ^a_a−1 ale a < a² −2a + 2 a < ^a_a−1ale a > a² −2a + 2 oraz a² −2a + 2 > ^a_a−1 ale a² −2a + 2 < a a² −2a + 2 < ^a_a−1 ale a² −2a + 2 >a

:P: jak nie rozumiesz, albo nie wiesz jak to napisz.