wzorek Kasienka: Funkcja kwadratowa, której wykres przechodzi przez punkty (0,−3),(1,−5),(−2,−11) jaki ma wzór? proszę o pomoc bo nie mogę rozkminić jak to zrobić

Mila: y=ax²+bx+c (0,−3) −3=0*a+0*b+c dalej postac iloczynowa

Mila: jak Ci idzie ?

Kasienka: Byłoby lepiej jak bym lubiła matmę a ja jej nie znosze

Mila: niechcący wprowadziłam cię w bład .c=−3 zeby obliczyc a i b układ równan trzeba zrobić

Kasienka: a jak on ma wyglądać?

Mila: y=ax²+bx+c y=ax²+bx−3 podstawiamy za x i za y (1,−5) (−2,−11) −5=a*1+b*1−3 −11=a*(−2)+b*(−2)−3 −5=a+b−3 −11=−2a−2b−3 można rozwiazać metoda podstawiania albo przeciwnych wspólczynników Dasz radę ?

Mila: Przepraszam nie podnosłam do kwadratu prawde mówiac chora jestem ale mnie ciagnie do zadan −5=a+b−3 −11=a(−2)²−2b−3 −5=a+b−3 −11=4a−2b−3

Mila: najlepiej metoda przeciwnych wspólczynników Pamietasz ją ?

Kasienka: staram się właśnie zrobić tą metodą...

Kasienka: Nie wiem czy dobrze ale u mnie a= ⁵₆

Kasienka: Teraz znowu wyszło m, że y = −3x² +1 − 3

Mila: pomnożyłam obie strony przez 2 −10=2a+2b−6 −11=4a−2b−3 −21=6a +0−9 −21+9=6a −12=6a −2=a

Kasienka: teraz wyszło mi chyba raczej dobrze, bo y = −2x² − 3

Mila: Dobrze a w tamtym zadaniu która odpowiedz zaznaczyłaś ?

Kasienka: y = 2(x+2)(x−5)

Mila:

Kasienka: a z przesunięć też jesteś dobra?

Mila: Nie wiem Napisz zadanie

Kasienka: wzór funkcji której wykres powstaje w wyniku przesunięcia wykresu funkcji y = ³₄x² − ¹₂x + ¹₄ o 1 jednostkę w lewo i 2 jednostki w dół jaka ma postać kanoniczną

Mila: jeżeli przesuwasz w lewo znak jest plus .w prawo znak minus w górę znak plus w dół znak minus

	3		1		1
y=		*x2−		x+
	4		2		4

	3		1		1
y=(		*x+1)2−		*(x+1)+		−2
	4		2		4

y=

Mila: oj niedobrze ze mna 3/4 poza nawiasem

Kasienka: tylko ja nie mam takiej odpowiedzi O.o odpowiedzi mam takie: y= ( x + ²₃ )² − 1⁵₆ y = ( x − 1¹₃)² + 2¹₆ y= ³₄(x+ ²₃)² − 1⁵₆ y = ³₄(x−1¹₃)² − 1⁵₆

Mila: kasiu naipierw przesuwamy wykres to w lewo ( prawo) piszemy kolo x to gora dół to wyraz wolny póżniej trzeba wszystko uproscić czyli masz skończyc to co napisałam

Kasienka: aaaaa to takie buty jaki tępak ze mnie

Mila: y=3/4(x+1)²−1/2(x+1)+1/4−2

	3
y=3/4(x2+2x+1)−1/2*x−1/2−1
	4

y=3/4*x²+3/2*x+3/4−...........

Mila: jak to zrobisz to napiszę co dalej

Kasienka: lepiej nie pytaj co mi wyszło

Mila: nie moze być aż tak zle pisz inaczej sie nie nauczysz

Kasienka: wyszło mi : y= ³₄ x² + x − ³₂

Mila: bardzo dobrze A teraz podaj wzór na postac kanoniczną

Kasienka: kanoniczna to y= a (x−p)²+q

Mila: p=

Kasienka: nie mam pojecia O.o

Mila: Kasiu p i q to współrzędne wierzchołka paraboli Zapamiętaj to bo jeszcze nie raz będzie ci potrzebne

	−b		−Δ
p=		q=		Δ=b2−4ac
	2a		4a

y=3/4*x²+x−3/2 a=3/4 b=1 c=−3/2

Kasienka: p mi wyszło −²₃ a q ³₆

Kasienka: z tego co widzę i wnioskuję to ma wyjść wynik końcowy y = ³₄(x+²₃)² −1⁵₆ tak mi podpowiada moja żyłka detektywistyczna

Mila: p dobrze q nie pokaz jak Δ policzyłaś

Kasienka: q = −^Δ_4a Δ= b² − 4ac Δ= 1 − 4*³₄*−³₂ Δ= 1 + 6 Δ= 7

Kasienka: co ja zrobiłam O.o ale błysnęłam inteligencją...

Mila: Δ=1−4ac Δ=1−4*3/4*(−3/2) Δ=1+3*3/2 Δ=1+9/2=11/2

Kasienka: ale żem błysnęła na prawdę inteligencją aż mi wstyd

Mila: Kasiu wyluzuj

Kasienka: 1⁵₆ wychodzi mi

Kasienka:

	3		2		5
czyli ten wzór to y =		(x+		)2 − 1
	4		3		6

Mila:

	5
− 1		czyli postac kanoniczna ....
	6

Mila: o juz napisałas

Kasienka:

	9
Oblicz dla jakich wartości parametru P równanie x2 + px + 2p +		=0 ma dwa rozwiązania,
	4

których suma jest mniejsza od 5

Bogdan: Po pierwsze nie piszemy: Δ = ... Δ = ... Δ = ... Δ = ... ale Δ = ... = ... = ... Oznaczenie literowe nie powtarzamy, jeśli mamy do czynienia z działaniem rachunkowym. Po drugie: p, q to współrzędne wektora przesunięcia paraboli lub innego obiektu, współrzędne wierzchołka paraboli oznaczamy x_w, y_w. Spotyka się niestety publikacje z oznaczeniem współrzędnych wierzchołka paraboli literkami p, q.

Mila: kiedy równanie kwadratowe ma 2 rozwiązania

Kasienka: wtedy kiedy Δ>0

Mila: dobrze Δ>0 policz Δ

Kasienka: wyjdzie 3?

Mila: napisz jak liczyłaś

Kasienka:

	9
Δ = p2 − 4*1*
	4

Δ = p² − 9 −p² = −9 p² = 9 p = 3

Mila: zgubiłaś 2p ono tez należy do c

Kasienka: ta? a tego to nie wiedziałam

Mila: koło x² jest a koło x jest b a reszta to c

Kasienka: to poczekaj teraz muszę zabłysnąć inteligencją i obliczyć to znowu

Kasienka: p = 2√2p −3 ?

Mila: zle pokaż Δ

Kasienka:

	9
Δ= p2 − 4*1* (2p +		)
	4

Δ = p² − 8p + 9 −p² = −8p + 9 p² = 8p − 9 p = √8p − 3 p = 2√2p − 3

Mila: przed nawiasem −4 czyli −9

Kasienka: o ja głupia cipa

Kasienka: czyli p = 2√2p + 3 ?

Mila: Δ=p²−8p−9 p²−8p−9>0 jezeli maja być dwa pierwiastki a=1 ( bo koło p²nic nie ma czyli jest 1) parabola będzie miała ramiona do góry.Jej czesc będzie pod osia y a reszta nad osia .nas interesuje tylko ta czesc nad osia bo tam P²−8p−9>0 (y>0 jest nad osia przeciez)Nad osia będzie dla x od −∞ do punktu gdzie parabola ma punkt przeciecia z osia OX czyli pierwiastka p₁ i od pierwiastka p₂ do nieskonczoności czyli teraz liczymy Δ i perwiastki z p²−8p−9=0

Kasienka: to Δ = 100 a x1 = −1 a x2 = 9

Mila: to dla jakiego p istnieją 2 pierwiastki

Kasienka: dla p>0

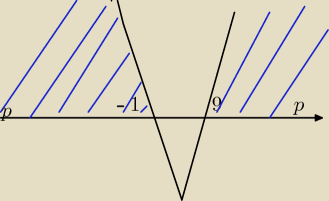
Mila: krzywe to ale chyba wiesz o co chodzi .Dla tych p istnieja 2 pierwiastki ale nas interesuje dla jakiech wartosci p x₁+x₂<5 Wzory Vieta sie kłaniaja

Kasienka: nie miałam jeszcze tych wzorów...

Mila:

	−b		c
x1+x2=		ten potrzebujemy jest jescze x1*x2=
	a		a

Kasienka: idę spać bo już nie uniese jutro jeszcze będę męczyć się tutaj z zadaniami dziękuję Ci i miłych snów Ci życzę

Mila: Kasiu moze streszczenie x²+px+2p+9/4=0 maja byc 2 pierwiastki czyli Δ>0 liczymy dla jakiego p Δ.>0 Δ>0 dla p∊(−∞,−1)u(9,∞) teraz musimy policzyc dla jakiego p suma pierwiastków<5

	−b
x1+x2=
	a

−b
	<5
a

−p
	<5
1

........

Mila: jutro moge nie mieć czasu −p<5 /*(−1) zmiana znaku p>−5 p∊(−5,∞) teraz wyznaczamy cześc wspólna( z tego co narysowałam) p∊[(−∞.−1)u(9,∞)] (−5,∞) p∊(−5.−1)

Pati: a nie czasem p∊(−5,−1) i (9,+∞) ?