Prosze bardzo o pomoc w zadanku na jutro . Malineczka: Prosze bardzo o pomoc w zadanku na jutro . Znajdz obraz prostej y= 1/3x+7 (ułamek) w translacji o wektor u=4,−3

Jack: znajdz dwa dowolne punkty spełniające pierwszą równość. Potem kazdy z nich poddaj translacji i z otrzymanych punktów odtwórz równanie nowej prostej

Malineczka: a mogłabym poprosic o pokazanie jak sie dokladnie rozwiazuje , krok po kroku ? Bardzo prosze .

Jack: napisałem wlasnie krok po kroku. Znajdź najpierw dwa punkty leżące na wyjsciowej prostej. Potem kazdy z nich przesuń o wektor. Potem z otrzymanych punktów odtwórz prostą która przez nie przechodzi.

Malineczka: oki , ale chodizło mi tak konkretniej o równanie które mozna by było to przedstawic i rozwiazac

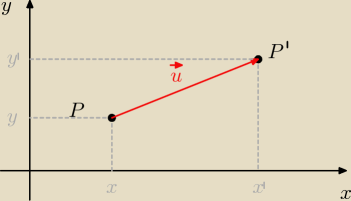
Trivial: Mamy dowolny punkt P = (x, y) i wektor u = (Δx, Δy). Wynikiem przesunięcia punktu P o wektor u jest punkt P' = (x', y'). Wyliczmy te współrzędne. P + u = (x, y) + (Δx, Δy) = (x + Δx, y + Δy) = (x', y') = P'. A zatem

	⎧	x' = x + Δx
	⎩	y' = y + Δy

P' = (x + Δx, y + Δy) Załóżmy teraz, że punkt P spełnia równanie funkcji f(x), czyli y = f(x). P = (x, f(x)). Dla punktu P' zachodzi P' = (x + Δx, f(x) + Δy). Ale chcemy wyrazić wyrazić drugą współrzędną jako funkcję argumentu x' = x + Δx, a więc P' = (x + Δx, f(x) + Δy) = (x', f(x + Δx − Δx) + Δy) = (x', f(x' − Δx) + Δy). Zatem funkcja postaci y₁ = f(x) po translacji o wektor u = (Δx, Δy) będzie miała wzór y₂ = f(x − Δx) + Δy. Oznacza to, że aby otrzymać nowy wzór należy za każdego x w równaniu funkcji podstawić (x − Δx) i do całości funkcji jeszcze dodać Δy. W tym zadaniu: Δx = 4, Δy = −3

	1		1
y1 =		x+7 → y2 =		(x−4)+7 + (−3)
	3		3

	1		4
y2 =		x −		+ 4
	3		3

	1		8
y2 =		x −		. (odpowiedź)
	3		3

Malineczka: Dziekuje bardzo za pomoc .