prosze o wszystkie rozwiązania do tego zadania mateusz 12345: oto zadanie : Które wyrazy ciągu (an) są ujemne.prosze o wszystkie rozwiązania do tego zadania i to jak najszybciej A) an =n²−5n−10 B) an=n²−11n+10 C) an 3n²−10n+8

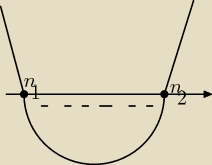
Ajtek: Rozwiąz nierówność: A) 0>n²−5n−10 Δ=65 √Δ=√65 − ciut więcej niż 8

	5−√65
n1=		≈−1,5 odrzucamy
	2

	5+√65
n2=		≈6,5
	2

Wiemy że n€N czyli wyrazy ujemne to: a₁, a₂, a₃, a₄, a₅, a₆.

mateusz 12345: dzięki a rozwiązesz mi pozostałe

mateusz 12345: a i jak obliczyłes delte?

Ajtek: Δ=b²−4ac . Pozostałe ładnie wyjdą zrobisz sam.

mateusz 12345: Ajtek cz w drugim przykładzie n1=−10 a n2= −1

mateusz 12345: a w trzecim przykładzie wyszło mi n1=2 a n2 = −1(3)

Ajtek: no nie, machnąłeś się w pierwiastkach:

	−b−√Δ		−b+√Δ
x1=		x2=
	2a		2a

mateusz 12345: nie no liczyłem 2 razy napisze ci jak rozwiązałem podpunkt B 0>n²−11n+10 Δ=11²−4*1*10=121−40=81 pierwiastek z Δ =9 x1=−11−9/2*1 =−10 x2=−11+9/2*1=−1

Ajtek: an=n²−11n+10 a=1, b=−11 c=10 Δ extra, pierwiastki bleee .

mateusz 12345: czyli n1=1 a n2=10 a jezeli nie to napisz mi jak to powino byc

Ajtek: Tak Teraz podaj wyrazy mniejsze od zera.

mateusz 12345: od a2 do a9 a w trzecim podpunkcie bedzie n1=1(3) a n2 =2

Ajtek: Wygląda, że tak . Które będą ujemne w trzecim?

mateusz 12345: w trzecim wydaje sie ze zaden z ciągów nie bedzie ujemny..

Ajtek: I niech tak zostanie, jak widzisz wcale nie było to straszne .

mateusz 12345: a pomozesz mi przy jeszcze jednym /oto zadanie które wyrazy ciągu (an ) sa równe zeru A) an=n³−4n²+n−4 kreska ułamkowa 2n²+4 B) an=(n³−64)(64−n²) kreska ułamkowa 3n−1

Ajtek:

	n3−4n2+n−4
an=
	2n2+4

To będzie zero w.t.w. kiedy licznik jest=0 n³−4n²+n−4=0 Z przykładem b pokombinuj, można tam coś zauważyć .

mateusz 12345: czyli w tym A to co bedzie rozwiązaniem

Ajtek: Podpowiem: (n³+n)+(−4n²−4)=0 Coś można wyciągnąć przed nawiasy .

mateusz 12345: n?

mateusz 12345: lub 4

mateusz 12345: szczerze jak bys mi to rozwiązał od deski do deski to był bym wdzięczny

Ajtek: i n i −4

mateusz 12345: jeszcze troche nie kumam prosze rozwiąz mi to

Ajtek: Z pierwszego n, z drugiego −4 n(n²+1)−4(n²+1)=0 Zauważ, że w obu nawiasach mamy to samo, czyli możemy znowu wyciągnąc przed nawias: (n²+1)(n−4)=0 (n−4) bo n stało przed pierwszym nawiasem, a −4 przed drugim. Iloczyn dwóch nawiasów =0 wtw kiedy jeden z nich będzie równy zero. I mamy: n²+1=0 n²=−1→ sprzeczność; n−4=0 → n=4 Dla n=44 tenciąg przyjmuje wartość 0. Rozumiesz?

mateusz 12345: rozumiem tak w 60 % a ten drugi przykład

Ajtek: Podpowiem tylko, drugi nawias to wzór skróconego mnożenia, trzeba go rozwinąć, a pierwszy też rozbić sprytnie. I bedziesz miał lioczyn nawiasów czyli jak w tym co zrobiłem. Warunek ten sam .

mateusz 12345: dobra dzięki wielkie za pomoc

Ajtek: Nie ma za co, więcej wiary we własne umiejętnośći. Najgorsze to podnieść ręce i powiedzieć "nie umiem".