bardzo mi zależy na obliczeniach allejandro: na średnicy AB pewnego koła wybrano punkt C różny od A i od B. po jednej stronie tej średnicy wykreślono półokrąg o średnicy AC , po drugiej półokrąg o średnicy CB. wiedząc że ^AB_BC=p, oblicz stosunek pól części koła na które dzieli go ta figura złożona z wykreślonych półokręgów

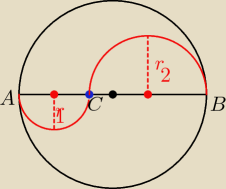
Basia: AB = 2R

	AC
r1 =
	2

	BC
r2 =
	2

P₁ = ¹₂πR² + ¹₂πr₁² − u{1}πr₂² P₂ = ¹₂πR² + ¹₂πr₂² − u{1}πr₁²

	AB
sprawdź czy na pewno ma być		=p, bo to sporo liczenia
	BC

	AC
pytam, bo byłoby prościej gdyby to było		=p
	BC

czekam na odpowiedź

allejandro: faktycznie jest AC i BC mój błąd, sory

Basia: no to mamy

r1		AC2		AC
	=		=		= p
r2		BC2		BC

r₁=p*r₂

	AC		BC		AC+BC		AB		2R
r1+r2 =		+		=		=		=		= R
	2		2		2		2		2

r₁+r₂ = R stąd p*r₂+r₂ = R r₂(p+1) = R podstawiamy do wzorów na P₁ i P₂ r₁ = p*r₂ R = (p+1)*r₂ P₁ = ¹₂πR² + ¹₂πr₁² − ¹₂πr₂²

	π
P1 =		*[ (p+1)2r22+p2r22 − r22 ]
	2

	πr22
P1 =		*[ p2+2p+1+p2−1]
	2

	πr22
P1 =		*[2p2+2p]
	2

	πr22
P1 =		*2p[p+1]
	2

P₁ = πr₂²*p(p+1) P₂ = ¹₂πR² + ¹₂πr₂² − ¹₂πr₁²

	π
P2 =		*[ (p+1)2r22 + r22 − p2r22 ]
	2

	πr22
P2 =		*[ p2+2p+1+1−p2]
	2

	πr22
P2 =		*[2p+2]
	2

	πr22
P2 =		*2[p+1]
	2

P₂ = πr₂²(p+1)

	P1
policz teraz
	P2

powinno wyjść p

allejandro: dzieki