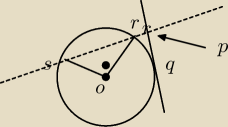kąty w okręgu
malaga0444: punkty Q ,R ,S leżą na okręgu o środku O i promieniu r. styczna do okręgu w punkcie Q przecina
prosta RS w punkcie P. Oblicz r jeśli :
a) |PQ|=4cm |PR|=2cm kąt ROS=90stopni
10 mar 14:51
:P:
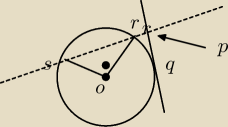
10 mar 22:25
:P: ma ktoś pomysł
10 mar 22:25
ICSP: chwilka

10 mar 22:26
10 mar 22:28
:P: ^^
10 mar 22:30
ICSP: 3√2?
10 mar 22:32
:P: twierdzenie 3. thx
|PQ|
2 = |PR| * |RS|
4
2 = 2 * |RS|
16 = 2 * |RS|
|RS| =
162 = 8
narazie mamy |RS| ale to już jesteśmy w domu.
zauważ, że trójkąt SRO to trójkąt prostokątny równoramienny o bokach długości "r" i podstawie
|RS|. Więc twierdzenie pitagorasa.
r
2 + r
2 = |RS|
2
2r
2 = 8
2
2r
2 = 64
r
2 = 32
r = 4
√2
Odp.: r = 4
√2
thx ICSP. dobrze

10 mar 22:36
ICSP: Twierdzenie dobre tylko troszkę źle zastosowane. Zauważ ze w tym twierdzeniu jest:
|PA| * |PB| a nie |PA| * |AB|.
10 mar 22:37
:P: a fakt ^^ jeszcze raz
10 mar 22:37
:P: 42 = |PR| * (|PR| + |SR|)
16 = 2 * (2 + |SR|)
16 = 4 + 2|SR|
2|SR| = 12
|SR| = 6
twierdzenie pitagorasa
62 = 2r2
36 = 2r2
r2 = 18
r = 3√2
thx
10 mar 22:41
ICSP: teraz już dobrze. Co prawda później można było liczyć z przekątnej kwadratu ale do twierdzenia
Pitagorasa również się nie przyczepią

10 mar 22:45