wyznaczanie elementow zbioru filip malczewski: wyznaczanie elementow zbioru tutaj zrzut: http://imgur.com/tk3zZ jak to wyliczyc?

filip malczewski: podbijam

filip malczewski: moze ktos pomoc ,nie za bardzo te zapiski rozumiem

filip malczewski: i jak bo zaraz mam zaliczenie, a chcialbym sie dowiedzieć

Bizon: i czegóż tam nie rozumiesz? .... w pierwszym .... co to liczby naturalne wiesz .... prostą nierówność też rozwiążesz ... i elementy wspólne znajdziesz (0,1,2,3) ... w drugim podobnie

komentator OWMH: Rozwiązanie : Dookoła nas istnieją rożne rodzaje zbiorów np. zbiór podręczników z języka francuskiego dla pierwszej klasy liceum, możemy jeszcze dokładnie określić dodając nazwę wydawnictwa Widać że w zwykłym codziennym życiu musimy określić jakiś zbiór dla naszej potrzeby. Możemy określić podając elementy z których się składa (lista elementów) lub określić podając cechy potrzebne do określenia dokładnie elementów tego zbioru. dobre określenie czegoś; jest potrzebny nam żeby ułatwić sobie życie, jak wiadomo człowiek jest jedynym zwierzęciem która musi pracować i uczyć całe życie; musi planować, analizować, konstruować, wybierać, selekcjonować, ryzykować , podejmować decyzje, ...itd. do tego jest potrzebne właśnie mieć trochę rozumu żeby cos zdefiniować i robimy to czasami opierając się na obserwacji swojego otoczenia. (warto jest być dobrym obserwatorem) od tego zależy czy dajemy radę , czy coś osiągniemy w życiu. Jak widać zbiory można określić dwoma sposobami; tak samo jest w matematyce. Zbiór jest pojęciem pierwotnym niedefiniowalnym; tylko można go określić. Mówimy że zbiór jest dobrze określony jeżeli znane są jego elementy lub znane jest kryterium pozwalające rozstrzygnąć czy dany element należy do tego zbioru czy też nie. Jak się podajemy elementy tego zbioru mówimy że zbiór jest określony ekstensywny. A jeżeli podane jest kryterium (cechy) pozwalające określić elementów tego zbioru mówimy się że zbiór zostało określone cechą ( za pomocą własnością) . Zbiory oznacza się dużymi literami A, B, C, itd. ; elementami małymi literami, a więc np. zbiór A składający się z elementów a, b, c, piszemy A = {a, b, c}; To że x jest elementem zbioru A zapisujemy x Є A; jeśli a nie należy to piszemy x ∉ A. Jeśli element x zbioru A określony jest za pomocą pewną formę zdaniową t o piszemy W(x); np. zbiór A który elementy należą do pewnego zbioru liczbowego G i równocześnie są określone przez formę zdaniową w(x) − warunek który spełniają wszystkie (i tylko) elementy tego zbioru; A zapisuje się : A = {x: x Є G i w(x)} albo też można napisać A = {x Є G: w(x)} W naszym zadaniu te zbiory są określone podając kryteria (przynależności do zbioru); które musi spełnić każdy element w swoim zbiorze; do zapisywania te kryteria używane są formy zdaniowe. Notacja ( inaczej Zapis umowny) ℕ₊ oznacza zbiór liczb naturalnych większych od zera tzn. ℕ₊ = {1, 2, 3, 4, 5, .......} ℂ₋ oznacza zbiór liczb całkowitych ujemnych. Wyznaczać elementy tych zbiorów oznacza określić tego zbioru podając te elementy. Wyznaczamy Zbiór A : A= { x Є N₊ i 3+4.x < 17} x jest liczbą naturalną różna od zera i jest rozwiązaniem nierówności 3 + 4.x < 17 rozwiązujemy nierówności 3+ 4.x <17 ⇔ x < 7/2 ⇔ x < 3¹₂ stąd x jest 1, 2, lub 3 a więc A = {1, 2 , 3} Wyznaczamy Zbiór B : B = { x Є ℂ₋ i −7 < x – 1 ≤ 5} x jest liczbą całkowitą ujemną , która spełnia nierówności −7 < x – 1 ≤ 5 stąd dodając na każdej strony 1 to otrzymamy −6 < x ≤ 6 , a więc x jest liczbą całkowitą ujemną którą znajduje się pomiędzy −6 i 6 oraz jest równy 6 tzn. x jest −5, −4, −3, −2, lub −1 stąd B = {−5, −4, −3, −2, lub −1}.

43ds: αβγδγΔΔδγδ

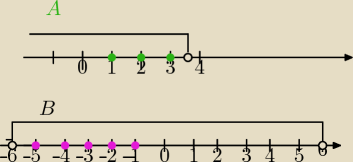
Mila: A={x :x∊N₊ i 3+4x<17} 4x<17−3 4x<14

	7
x<
	2

A={1,2,3} x>−6 i x<6 i x∊C₋ B={−5,−4,−3,−2,−1}

Mila: W tak długim komentarzu nie zauważyłam rozwiązania.

kazek: x²−2=0

kazek: podaj elementy zbioru ?

anonim: x ∊ℕ≤10