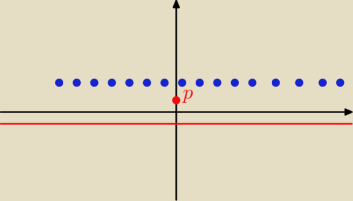
matura tralala: Mógłby ktoś mi wytłumaczyć to zadanie:

	1		1
Punkty równoodległe od prostej o równaniu y= −		i punktu P − (0,		) należą do
	2		2

wykresu funkcji f. Znajdź wzór tej funkcji. Powyżej narysowałem przykładowy wykres jakby to miałoby wyglądać.Za bardzo nie rozumiem "równoodległe" − myślę, że to tak samo jak "równoległe" − czyli te niebieskie kropki co narysowałem to chyba to tak?

tralala: Pomocy

jo: Równoległe to nie to samo co równoodległe (czyli w równej odległości od...). Niebieska kropka na osi y jakie ma współrzędne?

tralala: Niebieskie kropki miały słuzyc tylko jako przykład, równoległych

tralala: Jakiś pomysł jak rozwiązać to zadanie?

tralala: Naprawdę chcę zrozumieć to zadanie

tralala: Takie trudne to zadanie?

jo: Dla mnie to będzie parabola...

tralala: jak to obliczyć odpowiedź znam

	1
y =		x2
	2

tralala: pomocy

jo: No to od razu pisz a nie taki rysunek tylko (podobny do punktów tworzących prostą)... Eh, po co komplikować sobie życie...

tralala: możesz to zadanie zrobić?

tralala: pomocy

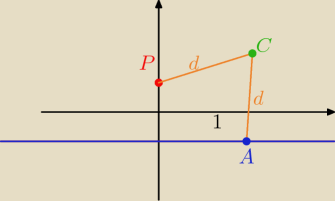
Eta: C(x,y) , P(0, ¹₂) , A( x, −¹₂) warunek: |PC|= |CA| i mamy: (x−0)²+(y−¹₂)² = (x−x)²+( y+¹₂)² x²+y²−y +¹₄ = y²+y + ¹₄ 2y= x²

	1
y=		x2 −−− wykresem jest parabola
	2

zbiór takich punktów C znajduje się na tej paraboli

tralala: Dziękuje bardzo http://www.kalkulatory.pl/blog/2009/11/28/probna-wpadka-operona/ Co sądzisz o tym ? Ma racje czy nie?

Eta: Też tak można .......... zalezy od "gustu"