trapez asia:

	3
W trapezie równoramiennym iloraz długości podstaw wynosi		. Wiadomo, że długość
	4

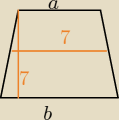
odcinka łączącego środki boków równa jest wysokości trapezu i wynosi 7 cm. Obliczyć promień okręgu opisanego na trapezie.

asia:

ICSP: Właśność trapezu równoramiennego:

a+b
	= 7
2

z treści zadania 3b = 4a. Reszta twoja.

Komar: ICSP: Skąd taka własność trapezu?;>

asia: dzięki. a umiałbyś mi to wytłumaczyc? https://matematykaszkolna.pl/forum/84173.html

ICSP: na pochodnych się nie znam.

asia: mam jeszcze jedno zadanie z geometrii. pomożesz?

ICSP: Jeśli będę wstanie...

Komar: Ponawiam pytanie: skąd taka własność trapezu? Nigdy o takiej nie słyszałam.

asia: Trójkąt ABC jest równoboczny o boku długości 1. Na bokach trójkąta wybrano punkty,K, L i M, tak

	AK		BL		CM
że		=a ,		=b i		=c . Ile wynosi pole trójkąta KLM?
	KB		LC		MA

AK, KB, BL, LC, CM, MA −są wektorami

ICSP: W wyniku takiego podziału powstały 4 identyczne trójkąty. równoboczne z których jeden to ten twój.

	1
bok twojego tójkąta :
	2

P trójkata równobocznego:

	a2√3		√3
P =		=
	4		16

chyba tak.

ICSP: A nie czekaj źle spojrzałem.

ICSP: Eta spojrzysz?

asia: hmm.. ja próbuje tak..

	1
KB=
	a+1

	1
LC=
	b+1

	1
MA=
	c+1

	a
AK=
	a+1

	b
BL=
	1+b

	c
CM=
	1+c

tylko co z tym dalej zrobić?

asia: a i mam 4 odpowiedzi do wyboru

	abc+1	√3
a)
	(a+1)(b+1)(c+1)	4

	abc	√3
b)
	(a+1)(b+1)(c+1)	4

	abc+1
c)
	(a+1)(b+1)(c+1)

	√3
d)abc
	4

asia: Eta pomóż proszę

Eta: Już jestem poprawna odp, to a) Nie bedę pisać, podam wskazówkę i sama dokończysz

	√3
PΔABC =
	4

PΔKLM = PΔABC − PΔAKM − PΔBKL −PΔCLM Pola każdego z tych trzech trójkątów liczysz ze wzoru

	1
		x*y*sin60o , gdzie x, y długości boków i między nimi kąt 60o
	2

zatem otrzymasz :

1

a

1

√3

√3

a

PΔAKM=

*

*

*

=

*

2

a+1

c+1

2

4

(a+1)(c+1)

i pozostałe podobnie ostatecznie otrzymasz:

	√3		a		b		c
PΔKLM=		( 1−		−		−		)=
	4		(a+1)(c+1)		(a+1)(b+1)		(b+1)(c+1)

sprowadź do wspólnego mianownika i otrzymasz:

	√3		(a+1)(b+1)(c+1) −a(b+1) − b(c+1) −c(a+1)
PΔKLM=		*
	4		(a+1)(b+1)(c+1)

dokończ ... wymnóż w liczniku, zredukuj i wyjdzie: odp: a)

Eta: Sorry, ale wczoraj nie zauważyłam tego postu

Eta: dla ICSP