:) M4ciek: Czy jest ktos chetny pomoc, bo chcialem pocwiczyc stereometrie

M4ciek: Podbijam

ICSP: No to ćwicz

M4ciek: ICSP dobrze ,ze jestes Chodzi mi konkretnie oto ,ze wstawisz mi ze 2−3zad. poziom R i je tu zrobie

morfepl: weź coś z kątem dwuściennym

ICSP: Jakie zadania kopnkretnie? Walce stożki kule, liczenie V za pomocą całki czy cos jeszcze innego?

M4ciek: Mam jutro sprawdzian − dzial stereometria Wiec od graniastoslupow po stozek.Wszystko co jest wymagane na maturze poziom R Cos bym chcial zrobic^^

ICSP: W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają taką samą długość. Oblicz cosinus kąta: zawartego miedzy sąsiednimi ścianami bocznymi.

M4ciek: Ok zabieram sie

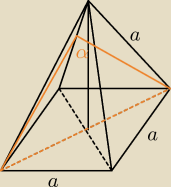
M4ciek: Dobrze narysowane

ICSP: Bardzo dobrze.

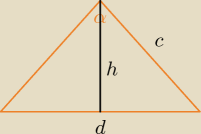
M4ciek: d = a√2

1		1   a√2 2
	sin α =
2		c

I nie wiem jak niestety policzyc c.

ICSP: Narysuj ścianę boczną

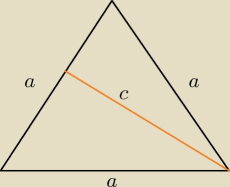
M4ciek: I tu bedzie :

	1
(		a)2 + c2 = a2
	2

ICSP: wiesz co to za trójkąt?

M4ciek: Ehh...

	a√3
c =
	2

ICSP: Tak c jest tyle równe. Wysokość trójkąta równobocznego sie kłania. Teraz to już prostę.

ICSP: Nie mogę zrozumień tego co napisałeś wyżej. Tego wzoru.

M4ciek:

	1		1   a√2 2
sin		α =
	2		a√2   2

= ... tak

M4ciek: No wole Ci tego nie tlumaczyc bo zle na to spojrzalem

ICSP: troszke tu naplątane i niepotrzebne. W zadaniu mamy napisane że trzeba obliczyć cosinus więc nie rozumiem toku rozumowania w którym liczymy sinus.

M4ciek: Ehh sorry... Wiec tak : Wyliczam z pitagorasa h w moim Δ.

	1		h
cos		α =
	2		c

tak

ICSP: Nadal nie to. Jesteś z klasy ogólnej czy rozszerzonej?

M4ciek: No niby rozszerzonej , ale zdaje 10 osob rozszerzenie...

ICSP: To w takim razie powinienes żnać dwa podstaowe twierdzenia stosowane przy rozwiazywaniu zadań ze stereometri dla klasy rozszerzonej: Twierdzenie: 1.cosinusów 2.sinusów

M4ciek: Znam oba ... Czemu nie moze byc tak jak napisalem

ICSP: podaj wzór na coinus połowy kąta.

M4ciek:

	1		h
cos		α =
	2		c

ICSP:

	α
ale jak byś chciał obliczyć cos jak byłs miał już cos
	2

M4ciek: Rozumiem o co Ci chodzi. Dobra juz wiem jak to policzyc , mam wszystkie boki Δ wiec z tw.cosinusow : (a√2)² = (a√3)² + (a√3)² − 2*(a√3)*(a√3)cosα

ICSP: Zapomniałeś o czymś

M4ciek: Czego

ICSP: Albo nie znasz wzoru na wysokość w trójkącie równobocznym albo nie chce ci sie pisać ułamków.

M4ciek: Nie dobra kompromitacja... Nastepne prosze

Godzio: W ostrosłupie prawidłowym czworokatnym pole kazdej z pieciu scian jest równe 1. Ostrosłup ten scieto w połowie wysokości płaszczyzną równoległą do podstawy. Obliczyc objetosc oraz pole powierzchni całkowitej otrzymanego ostrosłupa scietego.

ICSP: Jak wyliczysz to podasz wynik. następne: W ostrosłupie prawidłowym czworokątnym wysokość jest równa 6 i tworzy z krawędzią boczną kąt 45^o. Ostrosłup ten przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem 60^o. Oblicz pole otrzymanego przekroju.

ICSP: Witamy Godzia. Ja na razie idę wziąć leki wiec nie będzie mnie przez chwilkę.

M4ciek: Dobra Godziu byl pierwszy to zaczne od tego.

M4ciek: Ok

Godzio : Witam

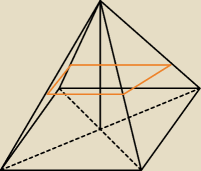
M4ciek: Obrazek kiepski , ale to tylko na kompie Drugie pole podstawy to tez kwadrat jakby co.

Godzio: ok

Ajtek: Oooo, widzę odpytka ochotnika przy tablicy . M4aciek powodzenia, a zadanie Godzia trudne nie jest . Chyba .

Godzio: Banalne można powiedzieć

Ajtek: W sumie to można w pamięci policzyć, nie robiąc rysunku. Chociaż h ostrosłupa będzie pod pierwiastkiem wychodzila.

M4ciek: Pp = a² 1 = a² a = 1

	1
Pb =		a*hsciany
	2

	1
1=		*1*hsciany
	2

	hsciany
1 =
	2

h_sciany = 2

	1
(		a√2)2 + H2 = (hsciany)2
	2

	1
(		*1*√2)2 + H2 = 22
	2

	1
H2 = 4 −
	2

H = √⁷₂

	√14
H =
	2

Narazie tyle

Godzio:

	√14
√4 − 12 =		?
	2

Godzio: Naczy to dobrze, ale wcześniej się walnąłeś

M4ciek: W skrocie pisze na spr. pisze normalnie

	√14
Hscietego =
	4

	1
V =		a2 * Hscietego
	3

	√14
V =
	12

Ajtek: 4−¹₂=⁷₂

	√7		√14
√72=		=		usunięta niewymierność z mianownika, czyż nie?
	√2		2

ICSP: Myślisz że krawedź podstawy ściętego jest równa krawędzi podstawy nieścietego?

M4ciek: Moment , ale ja mam policzyc scietego czyli tego na dole

Godzio: Ale teraz to nie jest ważne, ty przyjąłeś że krawędź boczna równa się krawędzie podstawy

ICSP: Możliwe że to jest dobrze, spytaj Godzia. Ja bym to troszkę inaczej zrobił.

M4ciek: To co mam zle bo ja juz nie rozumiem

M4ciek: Bo zostalo mi policzyc Pole tego scietego czyli tego na dole tak

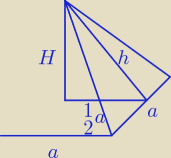
Godzio: a = 1, h = 2 Licz

M4ciek: Moment , ale ja mam policzyc ten na dole tak

M4ciek:

	1		1
V =		Pp *		H
	3		2

	1		√14
V =		*1*
	3		4

	√14
V =
	12

M4ciek: To jest ok

Godzio: To jest wskazówka Myśl ! Ja teraz wychodzę, będę wieczorem i sprawdzę Twoje dokonania

	17		7√15
Odp: Pc =		, V =
	4		48

Masz obliczyć objętość stożka ściętego − tego o 2 podstawach

M4ciek: Aaa... Dobra tylko jak sie ma bok Pola mniejszego do tego na dole rownego 1

ICSP: może z twierdzenia talesa spróbuj.

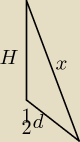
M4ciek: d = a√2 = √2

	1
(		d)2 + H2 = x2
	2

	1		√14
(		*√2)2 + (		)2 = x2
	2		2

1		14
	+		= x2
2		4

16
	= x2
4

	4
x =		= 2
	2

z − bok gornej podstawy

x		1   x 2
	=
a		z

	1
2 =
	z

2z = 1

	1
z =
	2

M4ciek:

	1
ICSP czyli bok gornej krawedzi wynosi
	2

M4ciek: bok gornej podstawy*

ICSP: Chyba tak.

M4ciek:

	1
2x +		= 1
	2

	1
2x =
	2

	1
x =
	4

	1
12 = (		)2 + h2
	4

15
	= h2
16

	√15
h =
	4

	(a+b)*h		1   √15   (1 + )*   2   4
Pb =		=
	2		2

	3√15
Pb =
	16

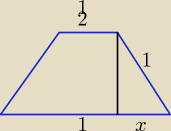
I Teraz Pole calego : P_c = 2Pp + 4Pb

	3√15
Pc = a2 + z2 + 4*
	16

	1		3√15
Pc = 1 +		+
	4		4

	5 + 3√15
Pc =
	4

Niestety odp. sie nie zgadza wiec czekam na Ciebie Godziu

ICSP: Jak jesteś na tyle szalony to możesz sie za moje zadanko zabrać

M4ciek: A objetosc :

	1		√14		√14
V = Pp *		H = 1 *		=
	2		4		4

M4ciek: Nie poczekam na razie na to Musze sie jutro przylozyc i takich glupich bledow nie robic jak np. pole Δ. Bo wszystkie wzory znam tylko kwestia sie skupic

Godzio: Już jestem, zaraz pokaże rozwiązanie

M4ciek: Wlasnie chetnie zobacze gdzie sie pomylilem bo czesc mam pewnie dobrze

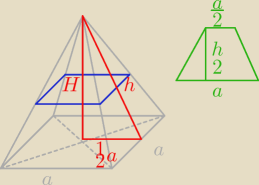
Godzio: P_p = a² = 1 ⇒ a = 1

ah
	= 1 ⇒ h = 2
2

	1		√15
H2 + (		)2 = h2 ⇒ H =
	2		2

	1		√15
Ostrosłup ścięto w połowie więc wysokość szukanej bryły to		H =
	2		4

	1		a   + a 2		h
Postrosłupa ściętego = a2 + (		a)2 + 4 *		*		=
	2		2		2

	1		17
= 1 +		+ 3 =
	4		4

	1		1		1		H
Vostrosłupa ściętego =		a2H −		* (		a)2 *		=
	3		3		2		2

	1		1		√15		7		7√15
=		a2H(1 −		) =		*		=
	3		8		6		8		48

M4ciek: Czemu mi to nie wyszlo ... Chcialbym jutro cos takiego dostac

Godzio: Zabieraj się teraz za zadanie ICSP

M4ciek: Troche pozno jest wiec juz nie dam rady , a nie moge isc niewyspany Dzieki za pomoc,Dobranoc

Godzio: W takim razie dobranoc i powodzenia na sprawdzianie