objetosc ostroslupa
maja: Oblicz objętość prawidłowego ostrosłupa czworokątnego w którym krawędz podstawy ma długość 4 a
kąt między dwoma sąsiednimi scianami bocznymi ma miare 120 stopni.
9 mar 17:17
ablikexe: Pp = 14a2√3 = 14*4*4*√3 = 4√3
Wysokość ostrosłupa, krawędź boczna i 23 wysokości podstawy tworzą trójkąt prostokątny
30,60,90.
Wysokość podstawy = 12a√3 = 2√3
Wysokość podstawy = wysokośc ostrosłupa * √3
Wysokość ostrosłupa = 2
V = 13*4√3*2 = 223√3
9 mar 17:23
maja: dziekuje!

9 mar 17:24
ablikexe: Dobra, to było rozwiązanie dla ostrosłupa trójkątnego

Źle przeczytałem...
Zaraz zrobię dla czworokątnego

9 mar 17:25
maja: ok

9 mar 17:28
ablikexe: P
p = a
2 = 4
2 = 16
Wysokość ściany bocznej, połowa krawędzi podstawy i wysokość ostrosłupa tworzą trójkąt
30,60,90.
Połowa krawędzi podstawy = wysokość ostrosłupa *
√3
Połowa krawędzi postawy =
12*4 = 2
| | 2 | | 1 | |
Wysokość ostrosłupa = |
| = |
| *2√3 |
| | √3 | | 3 | |
| | 1 | | 1 | | 5 | |
V = |
| *16* |
| *2√3 = 3 |
| √3 |
| | 3 | | 3 | | 9 | |
9 mar 17:32
ablikexe: Dobra, ja jakiś nieprzytomny jestem

Najlepiej niech to ktoś inny policzy. Bo ja już chyba
nie myślę

Przepraszam, ale to drugie rozwiązanie chyba też jest złe. Idę odpocząć.
9 mar 17:37
maja: mimo wszystko dziekuje

9 mar 18:01
Ajtek:
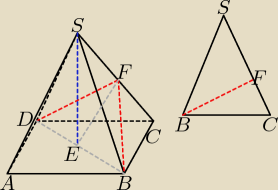
|AB|=|BC|=|CD|=|AD|=4
≤) DFB=120
o → ≤) EBF=30
o
|BD|=4
√2 → |BE|=2
√2
W Δ BEF:
|BF|=
43√6
Z Δ BCF wyliczam |CF|:
|CF|
2=|BC|
2−|BF|
2
|CF|=
43√6
I tutaj staję, coś nie tak jest, tylko nie wiem co, hmmmm.
9 mar 18:51
ablikexe: Opierając się na Twoich obliczeniach (i rysunku):
X to środek odcinka BC
(
12|BC|)
2+|SX|
2 = |SC|
2
2
2+|SX|
2 = |SC|
2
|SX|
2 = |SC|
2−4
12*|BC|*|SX| =
12*|SC|*|BF|
2*|SX| =
23√6*|SC|
4*|SX|
2 =
49*6*|SC|
2
4*(|SC|
2−4) =
83*|SC|
2
4*|SC|
2−16 =
83*|SC|
2
1
13*|SC|
2 = 16
13*|SC|
2 = 4
|SC|
2 = 12
|SC| = 2
√3
|SX|
2 = 12−4
|SX|
2 = 8
|SX| = 2
√2
|SE|
2+2
2 = |SX|
2
|SE|
2 = 8−4
|SE| = 2
V =
13*16*2 = 10
23
Powinno być dobrze

9 mar 19:29
9 mar 19:33

 Źle przeczytałem...
Zaraz zrobię dla czworokątnego
Źle przeczytałem...
Zaraz zrobię dla czworokątnego 

 Najlepiej niech to ktoś inny policzy. Bo ja już chyba
nie myślę
Najlepiej niech to ktoś inny policzy. Bo ja już chyba
nie myślę  Przepraszam, ale to drugie rozwiązanie chyba też jest złe. Idę odpocząć.
Przepraszam, ale to drugie rozwiązanie chyba też jest złe. Idę odpocząć.

 |AB|=|BC|=|CD|=|AD|=4
≤) DFB=120o → ≤) EBF=30o
|BD|=4√2 → |BE|=2√2
W Δ BEF:
|AB|=|BC|=|CD|=|AD|=4
≤) DFB=120o → ≤) EBF=30o
|BD|=4√2 → |BE|=2√2
W Δ BEF:




