? karola: Oblicz pole rombu o boku 17cm, w którym długości przekątnych różnią się o 14 cm

M:

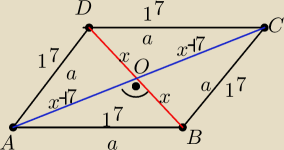
Podstawy Geometrii: | AC=q=2x+14 x>0 BD=p=2x x>0 AB=a=17 W trójkącie AOB (x+7)²+x²=17² x²+14x+49+x²=289 2x²+14x−240=0 x²+7x−120=0 Δ=49+480=529 √529=23

	−7−23
x1=		=−15 (nie należy do zbioru rozwiązań
	2

	−7+23
x2=		=8 >0
	2

q=2x+14 q=2*8+14=30 p=2x=2*8=16

	p*q
P=
	2

	16*30
P=		=240 cm2
	2

rąbek:

	fe
f,e −− dł. przekątnych f−e=14 , a= 17 −− dł. boku P=
	2

w każdym rombie : f²+e²=4a² f²+e²=(f−e)²+2fe to (f−e)²+2fe=4*289 14*14+2fe=4*289 / :4

	fe
49+		=289
	2

P= 240