lalalalala
lalalalala: Kto umie wyznaczyć największą i najmniejszą wartość funkcji
f(x)=x3−9x2+24x−10
na przedziale [0,3]?
8 mar 21:42
Malinka: musisz policzyć wartości funkcji z brzegów przedziału
oraz pochodną o ile miałaś pochodne funkcji
8 mar 21:45
student: Potrafisz policzyć?
8 mar 21:58
lalalalala: Tak, ale wynik nie zgadza się z odpowiedzią.
f'(x)=3x
2−18x+24
Miejsce zerowe pochodnej to x=4, x=2, 4 nie należy do przedziału.
No to liczymy:
f(0)=0−0+0−10=−10
f(2)=8−9*4+24*2−10=10
f(3)=27−9*9+24*3−10=8
W odp. wartość największa f(3)=62


8 mar 21:59
Malinka:
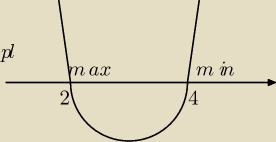
f(0)=−10
f(3)=27−81+72−10=8
f'(x)=3x
2−18x+24
f'(x)=0
3x
2−18x+24=0 \:3
x
2−6x+8=0
Δ=36−32=4
x
1=2
x
2=4
f(2)=10
f(4)=6
Najmniejsza wartość f wynosi −10 dla x=0
Największa wartość f wynosi10 dla x=2
8 mar 22:00
student: Skąd Ci się wzięło f(3)=62?
8 mar 22:02
student: O Malinka Ci już rozwiązała

8 mar 22:03
lalalalala: W odpowiedziach tak jest, skąd im się wzięło to nie mam pojęcia zielonego, ale wygląda na to,
że jest błąd

8 mar 22:03
Asdam: da się to bez pochodnych polioczyć
8 mar 22:03
Asdam: 
8 mar 22:03
lalalalala: Mi też wychodzi jak Malince
8 mar 22:03
Malinka: Nie mam pojęcia, na moje rozumowanie to nic innego jak błąd w książce, może ktoś inny znajdzie
na to sposób. Dla mnie największa dla f(2)=10

8 mar 22:05
student: Rozwiązanie jest prawidłowe

8 mar 22:07
lalalalala: Jak dla mnie też, same błedy tam są, człowiek się 5 godzin zastanawia co jest źle i się okazuje
że dobrze

8 mar 22:07
student: No niestety tak czasem bywa

.
8 mar 22:08
Shadow520:
zadanie jest dobrze rozwiązane wystarczy sprawdzić w excel'u i narysowac wykres
9 mar 10:39


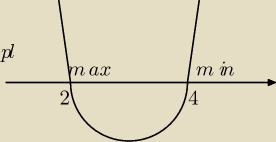 f(0)=−10
f(3)=27−81+72−10=8
f'(x)=3x2−18x+24
f'(x)=0
3x2−18x+24=0 \:3
x2−6x+8=0
Δ=36−32=4
x1=2
x2=4
f(2)=10
f(4)=6
Najmniejsza wartość f wynosi −10 dla x=0
Największa wartość f wynosi10 dla x=2
f(0)=−10
f(3)=27−81+72−10=8
f'(x)=3x2−18x+24
f'(x)=0
3x2−18x+24=0 \:3
x2−6x+8=0
Δ=36−32=4
x1=2
x2=4
f(2)=10
f(4)=6
Najmniejsza wartość f wynosi −10 dla x=0
Największa wartość f wynosi10 dla x=2






 .
.
 zadanie jest dobrze rozwiązane wystarczy sprawdzić w excel'u i narysowac wykres
zadanie jest dobrze rozwiązane wystarczy sprawdzić w excel'u i narysowac wykres