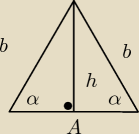
 Jeśli to Obwód ma być rowny 100√3 to wtedy:
A = 20√3
b = ?
Obw. = 100√3
α − kąt przy podstawie
100√3 = a + 2b = 20√3 + 2b
2b = 80√3
b = 40√3
możemy policzyć wysokość z twierdzenia pitagorasa.
h2 + 12A2 = b2
h2 + (10√3)2 = (40√3)2
h2 = 4800 − 300 = 4500
h = 30√5
P − pole trójkąta
P = 12 * 20√3 * 30√5 =300√15
sinα = hb = 30√540√3 = 1200√154800 = √154 ≈ 0,968245837
i wtedy α ≈ 83,91 ≈ 84 stopnie.
ale nie wyszedł dokładny wynik, czyli jednak chyba nie chodziło o obwód.
Jeśli to Obwód ma być rowny 100√3 to wtedy:
A = 20√3
b = ?
Obw. = 100√3
α − kąt przy podstawie
100√3 = a + 2b = 20√3 + 2b
2b = 80√3
b = 40√3
możemy policzyć wysokość z twierdzenia pitagorasa.
h2 + 12A2 = b2
h2 + (10√3)2 = (40√3)2
h2 = 4800 − 300 = 4500
h = 30√5
P − pole trójkąta
P = 12 * 20√3 * 30√5 =300√15
sinα = hb = 30√540√3 = 1200√154800 = √154 ≈ 0,968245837
i wtedy α ≈ 83,91 ≈ 84 stopnie.
ale nie wyszedł dokładny wynik, czyli jednak chyba nie chodziło o obwód.