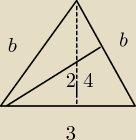
 linia przerywana to wysokość
Pt − pole trójkąta
Pt = 123*h = 12b*2,4
Wynika to z tego, że Pole trójkąta = 12*podstawa*wysokość opuszczona na tą podstawę
3020h = 2420b
30h20 = 24b20
600h = 480b
h = 45b
b2 = (45b)2 + (1,5)2
b2 = 1625b2 + 2,25
925b2 = 2,25
b2 = 2,25 * 259
b2 = 6,25
b = 2,5
wyszło, że ramię ma 2,5 długości
Twierdzenie Pitagorasa
(2,5)2 = h2 + (1,5)2
6,25 = h2 + 2,25
h2 = 4
h = 2
Odp. Wysokość = 2.
Sprawdźmy czyby się zgadzało:
Pt = 12*3*2 = 3
Pt = 12*2,5*2,4 = 3
zgadza się.
linia przerywana to wysokość
Pt − pole trójkąta
Pt = 123*h = 12b*2,4
Wynika to z tego, że Pole trójkąta = 12*podstawa*wysokość opuszczona na tą podstawę
3020h = 2420b
30h20 = 24b20
600h = 480b
h = 45b
b2 = (45b)2 + (1,5)2
b2 = 1625b2 + 2,25
925b2 = 2,25
b2 = 2,25 * 259
b2 = 6,25
b = 2,5
wyszło, że ramię ma 2,5 długości
Twierdzenie Pitagorasa
(2,5)2 = h2 + (1,5)2
6,25 = h2 + 2,25
h2 = 4
h = 2
Odp. Wysokość = 2.
Sprawdźmy czyby się zgadzało:
Pt = 12*3*2 = 3
Pt = 12*2,5*2,4 = 3
zgadza się.
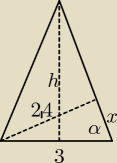 Trójkąt na rysunku P nie jest równoramienny. Jeszcze jeden mądrala udzielający rad
i lekceważący rysunek.
x = √32 − 2,42 = 1,8
Trójkąt na rysunku P nie jest równoramienny. Jeszcze jeden mądrala udzielający rad
i lekceważący rysunek.
x = √32 − 2,42 = 1,8
| h | 2,4 | |||
tgα = | = | |||
| 1,5 | 1,8 |
| 1,5 * 2,4 | ||
h = | = 2 | |
| 1,8 |