 1/ o: ( x−3)2 +y2=9 S(3,0) r= 3
l: x−y+9=0
oblicz odległość d punktu s od prostej l
jeżeli :
d=r=3 −−− prosta styczna
d>r >3 −−− prosta nie ma punktów wspólnych z okręgiem
d <r<3 −−− prosta precina okrag w dwu różnych punktach
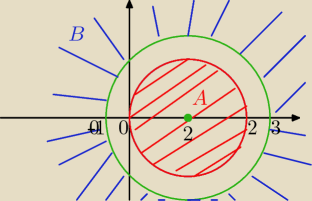
2/ zb.A to koło : (x−2)2 +y2≤ 4 , S( 2, 0) , r=2
zb. B zewnętrze koła( bez linii okręgu ; S(2,0) , r= 3
1/ o: ( x−3)2 +y2=9 S(3,0) r= 3
l: x−y+9=0
oblicz odległość d punktu s od prostej l
jeżeli :
d=r=3 −−− prosta styczna
d>r >3 −−− prosta nie ma punktów wspólnych z okręgiem
d <r<3 −−− prosta precina okrag w dwu różnych punktach
2/ zb.A to koło : (x−2)2 +y2≤ 4 , S( 2, 0) , r=2
zb. B zewnętrze koła( bez linii okręgu ; S(2,0) , r= 3
 x2 + y2 − 4x ≤ 0
wyobraź sobie, że jest to równanie prostej −−−> x2 + y2 − 4x = 0 i przekształcimy to tak
x2 − 4x + y2 = 0 //// do obu stron dodamy 4 tak aby powstał później wzór skruconego
mnożenia
x2 − 4x + 4 + y2 = 4
(x − 2)2 + y2 = 4
i teraz jest to koło o środku S = (2,0) i promieniu 2 zgodnie z wzorem
http://www.bazywiedzy.com/rownanie-okregu.php
i teraz to ma być ≤ 0
mniejsze czyli zamalowujemy to co w srodku
na rysunku
x2 + y2 − 4x ≤ 0
wyobraź sobie, że jest to równanie prostej −−−> x2 + y2 − 4x = 0 i przekształcimy to tak
x2 − 4x + y2 = 0 //// do obu stron dodamy 4 tak aby powstał później wzór skruconego
mnożenia
x2 − 4x + 4 + y2 = 4
(x − 2)2 + y2 = 4
i teraz jest to koło o środku S = (2,0) i promieniu 2 zgodnie z wzorem
http://www.bazywiedzy.com/rownanie-okregu.php
i teraz to ma być ≤ 0
mniejsze czyli zamalowujemy to co w srodku
na rysunku
| |A*xo+B*yo+C| | ||
d= | ||
| √A2+B2 |
| | 1*3 −1*0+9| | 12 | |||
d= | = | = 6√2 > 3
| ||
| √12+12 | √2 |
