F.liniowa Afrodyta: Oblicz pole trójkąta ograniczonego prostą y=−3x+2 oraz osiami układu współrzędnych Zrobicie mi to ? bo mam wiele zadań zadane a tego akurat nie umiem z góry dziękuję. i jak bym mogła prosić o objaśnienie każdego kroku,abym to zrozumiała

Ajtek: Musimy znaleźć punkty przecięcia się tej funkcji z osiami OX i OY. Punkt przecięcia z osią OX ma współrzędne (x;0), natomiast z osią OY (0;y). Czyli miejsce przecięcia z osią OX: y=−3x+2 w miejsce y wstawiamy 0 i obliczamy x Miejsce przecięcia z osią OY y=−3x+2 w miejsce x wstawiamy 0 i obliczamy y. To na początek, rozumiesz?

Afrodyta: Tak wiem jak to zrobić a co doalej ? Pomożesz mi ? i dziękuję

Ajtek: Policzone to mamy?

kobieta:

	1		2
P=		*3*		= 1 [j2]
	2		3

Afrodyta: Ajtek pomożesz mi. ? Tak tamto wyliczyłam .

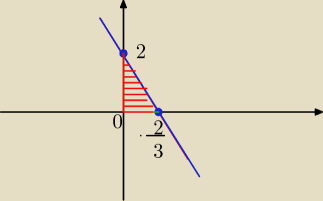
Ajtek: Już jestem, pomogę . Mój rysunek będzie przydatny nieco później. Wykorzystajmy do tego powyższy rysunek kobiety. Mam nadzieję, iż kobieta nie zarząda tantiem od praw autorskich . Wiemy, że nasze punkty przecięcia wykresu funkcji z osiami układu (0;2) i (²₃;0} są jednocześnie wierzchołkami trójkąta. Trzecim wierzchołkiem jest początek uładu współrzędnych, czyli punkt (0;0). Teraz musimy znaleźć długość podstawy i wysokość tego Δ. Możemy to odczytać z przywołanego rysunku kobiety. Odcinek na osi OX potraktujemy jako podstawę, (nazwijmy go a Δ), natomiast odcinek na osi OY jako wysokość (nazwijmy go h Δ). Odczytujemy z wykresu długość podstawy "a" i widzimy, że wynosi ona ²₃, identycznie odczytujemy wysokość "h" czyli 2. Podstawiamy do wzoru na pole Δ i mamy: P=¹₂*²₃*2=²₃ [jmp] [jmp] − jednostek miary pola, np.: mm², cm², m² itp. . Na długość odcinka są jeszcze wzory, ale to na osobną lekcję zostawimy . A może nie : Wzór na długość odcinka |AB|: d_AB=√(x_b−x_a)²+(y_b−y_a)², gdzie: d_AB − długość odcinka AB, x_a − współrzędna x punktu A, x_b − współrzędna x punktu B, y_a − współrzędna y punktu A, y_b − współrzędna y punktu B. Powyższy wzór do zapamiętania Zastosujmy ten wzór w naszym zadaniu: W tej chwili wiadomo, po co taki rysunek u mnie się pojawił . 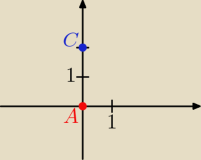Niech punkt A ma współrzędne (0;0), a C (0;2). Z założeń wcześniejszych po osi OY odczytywaliśmy wysokość czyli "h" naszego Δ, która wynosiła 2. Teraz podstwaiając do wzoru na długość odcinka "d" mamy takie coś: d_AC=√(0−0)²+(2−0)²=√0²=2²=√4=2. To by było na tyle na tą chwilę . Mam nadzieję, iż troszeczkę rozjaśniłem.

Eta:

krystek: ot kultura!