Stereometria Przemek: Proszę o pomoc! Podstawą graniastosłupa prawidłowego czworokątnego została wpisana w koło o średnicy 6√3. Oblicz v i pc wiedząc że kąt z płaszczyzną podstawy ma miarę 30 stopni. Proszę o szczegółowe rozwiązanie.

Ajtek: Graniastosłup prawidłowy czworokątny, w podstawie jest kwadrat. Narusuj kwadrat, opisz na nim koło, zaznacz średnicę i wyciągnij wniosek dot. długości przekątnej tego kwadratu. I napisz jeszcze o jaki kąt chodzi. Nie lubię się domyślać .

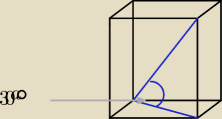
Przemek: Ajtek oblicz v i pc wiedząc że kąt jaki tworzy przekątna graniastosłupa z płaszczyzną podstawy mam miarę 30 stopni. sorki że nie dopisałem. Możesz mi to pokazać jak to obliczyć bo to co mi napisałeś to nie wiem jak zrobić. Będę bardzo wdzięczny.

adrian: a√2=6√3 a = 3√6 a wysokość graniastosłupa oblicz z tg30

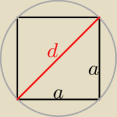
Ajtek: Tak wygląda kwadrat i opisany na nim okrąg. Wiemy, że średnica okręgu jest przekątną tego kwadratu i wynosi 6√3. Wiemy też, że przekątna kwadratu d=a√2, gdzie a to bok kwadratu. Czyli możemy zapisać coś takiego: d=a√2 i jednocześnie d=6√3 → a√2=6√3 z tego wyliczymy a:

	6√3		6√6
a=		=		=3√6
	√2		2

Wszystko jasne jak do tej pory

Przemek: Ajtek Tak moge ci napisać jeszcze jedno zadanie

Ajtek: No wal, tylko nie wiem czy dam rade .

Przemek: −W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 6 cm a kąt jaki tworzy krawędź boczna z wysokością ma miarę 60 stopni.Oblicz v i pc.

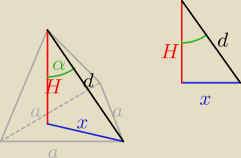
Ajtek: Mało wyraźny rysunek mi wyszedł.

	a√3
W podst. Δ równoboczny → h podst.
	2

	2
Odcinek x to		h Obliczyć x
	3

Teraz z Δ o bokach na rysunku dxH wyznaczmy H:

	2x√3   3
Ten Δ ma kąty 30, 60 i 90 zatem H=
	2

Trochę skomplikowanie to wygląda, ale trochę się spiesze. Mam nadzieję, że nie walnąłaem się w wyznaczaniu H.

Ajtek: Zapomniałem napisać a=6, natomiast α=60^o

Przemek: Tak oblicz mi x bo nie wiem jak to co mi napisałeś to dla mnie czarna magia