Funkcja kwadratowa Patryks: Dla jakich wartości parametru p równanie |x − 15| = p³ − 4p ma dwa rozwiązania, których iloczyn jest liczbą dodatnią?

Malinka: x−15=p³−4p lub x−15=−p³+4p x=p³−4p+15 lub x=−p³+4p+15 1. p³−4p+15>0 i −p³+4p+15>0 lub p³−4p+15<0 i −p³+4p+15<0

Patryks: Dlaczego w pierwszym przypadku większe od zera a w drugim mniejsze od zera ?

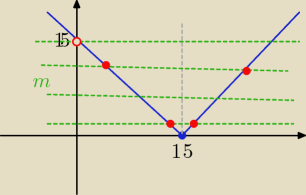
Eta: | t |= m to m>0 −−− wtedy są dwa pierwiastki 1^o p³−4p >0 ten drugi warunek widzisz na wykresie ( obydwa rozwiązania mają być dodatnie 2^o m€( 0, 15) to 0< p³−4p < 15 => p³−4p >0 i p³ −4p < 15 jako odp: podaj część wspólną warunków: 1^o i 2^o

Malinka: skoro w zadaniu jest mowa o iloczynie dodatnim tzn przy mnożeniu dwa minusy lub dwa plusy dają dodatnią wartość, dlatego dwa warunki

Malinka: do tych obu warunków dochodzi p³−4p>0 wynika to z warunku wartości bezwględnej Eta podała bardzo fajne i szybkie rozwiązanie

Patryks: Ok dzięki wielkie już rozumiem Powiedzcie mi jeszcze tylko jak rozwiązać p³−4p<15 bo nie umiem

Eta: p³−4p −15<0 W(3) = 27 −12 −15=0 podziel p³ −4p −15 przez ( p−3) ( p−3)(p²+3p +5) <0 Δ<0 zatem p−3 <0 => p <3

Malinka: wykonać trzeba dzielenie wielomianu: p²+3p+5 −−−−−−−−−−−−−−−−−−−−−−−−−− (p³−4p−15):(p−3) −p³+3p² −−−−−−−−−−−−−− = 3p²−4p−15 −3p²+9p −−−−−−−−−−−−− = 5p−15 −5p+15 −−−−−−−−−−− (p−3)(p²+3p+5)<0

Eta:

Malinka: