wymiary basenu Domii: basen w kształcie prostopadłościanu ma mieć pojemność 36 m³. Jego dno jest prostokątem, ktorego stosunek długości boków wynosi 2. Dno basenu i jego ściany chcemy wyłożyć kafelkami. jakie powinny być wymiary basenu, aby zużyć najmniej kafelków pomóżcie

:P: spróbujmy tak jeżeli podstawa ma 3 m i 6m P_p = 18 i wtedy H=2 V = P_p * H wtedy P_p = 18 i Pole boczne = 2*3*2 + 2*6*2 = 12+24 = 36 [cm²] jeżeli podstawa ma 2 i 4 to P_p = 8 H = ^V_Pp = 4,5 wtedy P_p = 2*2*4,5 + 2*4*4,5 = 18+36 = 54[cm²] czyli widzimy, że jeśli wysokość jest większa to trzeba więcej [cm²] czyli więcej kafelków i teraz pytanie jak małe może być H V = a*2a * H = 2a²*H = 36 2a² + 2*a*H + 2*2a*H = 2a² + 2aH (1+2) = 2a² + 6aH i to musi być najmniejsze z 1 wynika ze 2a² = ³⁶_H podstawmy ³⁶_H + 6aH /*H 36 + 6aH² a²*H = 18 a² = ¹⁸_H a = √¹⁸_H 36 + 6√¹⁸_H*H² <−−− i ta liczba musi być jak najmniejsza 36 zawsze będzie 36 wszystko tyylko zależy od H niewiem teraz może sprubujmy podstawić coś za H i wywnioskujemy

:P: ej sorka to jest źle nie pisz tego ^^

Domii: oo masz moze iny pomysł na to

:P: V = a*2a*H = 2a²H = 26 2a² + 2aH + 4aH = 2a² + 6aH z 1 wynika 2a² = ³⁶_H a = √¹⁸_H ³⁶_H + 6√¹⁸_HH i sprubuj sobie teraz wyliczyć, np. dla H=1, H=1,5, H=2, H=3 ja mam takie wyniki dla H = 1 to ³⁶_H + 6√¹⁸_HH ≈ 61 dla H = 2 to ³⁶_H + 6√¹⁸_HH = 54 dla H = 3 to ³⁶_H + 6√¹⁸_HH ≈ 56 dla H = 4 to ³⁶_H + 6√¹⁸_HH ≈ 59,91 i z tego by wynikało, że dla H = 2 jest najmniejsze Pole podstawy + Pole Boczne spróbuj sobie jeszcze może dla H = 2,5 i H = 1,5 żeby sprawdzić, żeby to było po prostu udowodnione. wtedy H = 2, a=3 b=6

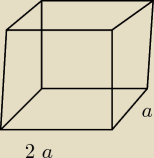
:P: w tym poście wyżej jest wszystko, tylko tam w pierwszej linijce ma być 36, a nie 26 H − wysokość a − jeden bok 2a − drugi bok sprubuj sobie przeanalizować, jak nie rozumiesz to pytaj. Pierwsze wyznaczam wzór na Objętość: V = Pole podstawy * Wysokość Pole Podstawy (prostokąt) = jeden bok * drugi bok V = a*2a*H = 2a²H Teraz wyznaczam Pole tego co chce obłożyć płytkami, czyli P = pole podstawy + pole 4 ścian bocznych basenu (z tym ze 2 są inne, a 2 inne)patrz rysunek P = a*2a + 2*pole ściany 1 + 2*pole sciany 2 pole ściany 1 = a*H (bo to też prostokąt) i pole sciany 2 = 2a*H P = 2a² + 2*a*H + 2*2a*H P = 2a² + 2aH + 4aH P = 2a² + 6aH i mamy te 2 wzory: V = 2a²H P = 2a² + 6aH z wzoru V wyznaczamy 2a² i a tak jak w poprzednim poście i podstawiamy do wzoru na P P = ³⁶_H + 6√¹⁸₁₈H no i podstawiamy sobie za H i pomału liczymy na kalkulatorze, wiadomo całe liczby nam nie wyjdą, więc zaokrąglamy

Domii: dzięki

Domii:

	36
a mam pyt.jeszcze, skąd się wzielo to ze Pp=		?
	H

:P: Objętość = Pole podstawy * Wysokość V = P_p * H i mamy 36 = P_p * H / dzielimy przez H P_p = ³⁶_H