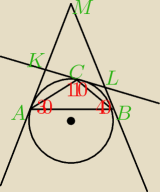
planimetria sk: Trójkąt ABC jest wpisany w okrąg o środku O, oblicz miary kątów wewnętrznych trójkąta KLM, utworzonego przez punkty przecięcia się stycznych do okręgu poprowadzonych w punktach A,B i C. na czerwono podane są katy przy każdym z wierzchołków

sk: re

sk: asd

sk: odswiezam

sk: i znowu...

sk: trudne to jest..

ICSP: kąt MBC = kątowi BAC kąt MAC = kątowi CBA

sk: z jakich własności to jest?

Oycho: Z tw. o kącie wpisanym i dopisanym: miara kąta LCB = 1/2 miary kąta BOC miara kąta LBC = 1/2 miary kąta BOC stąd LCB = LBC → ozn. α miara kąta KCA = 1/2 miary kąta AOC miara kąta KAC = 1/2 miary kąta AOC sta KCA = KAC → ozn. β |AO| = |OB| gdyż są to promienie; stąd: miara kąta ABO = miara kąta BAO → ozn. γ Jako, że promień okręgu poprowadzony do punktu styczności okręgu z prostą tworzy z tą prostą kąt prosty: α+40+γ=90 α+γ=50 (1) β+30+γ=90 β+γ=60 (2) w trójkącie AOB: 180−2γ=2α+2β 90−α−β=γ (3) Podstawiam γ do równań 1 i 2 α+90−α−β=50 β+90−α−β=60 β=40 α=30 w trójkacie LCB: miara kąta CLB = 180−60=120 w trójkacie KCA: miara kąta AKC=180−80=100 stąd: miara kąta MKL = 80 miara kąta MLK = 60 więc KML = 40 Miary kątów wewnętrznych to: 80, 60, 40