funkcja Pająk: podaj przedziały monotoniczności funkcji f(x)= −2x+3 / 2x−1 nie szkicując jej wykresu. zapisz równanie asymptoty poziomej funkcji

GrzesiekOPOLE: boze czego was ucza w tej szkole. . .szczere wspolczucia

Pająk: pewnie nie jest takie trudne tylko trzeba wiedzieć od czego zacząć, a ja tego nie wiem

Eta: D_f= R \ {¹₂}

	−(2x−1)+2		2
f(x)=		= −1 +
	2x−1		2x+1

asymptota pozioma : y= −1 asymptota pionowa: x = ¹₂ f(x) maleje : dla x€( −∞, ¹₂), x€ ( ¹₂, ∞)

romuland:

	1
dziedzine musisz określić (x≠		)
	2

i teraz musimy znaleźć w jakich ćwiartkach ta funkcja sie znajduje. Spróbuj przekształcić wzór tak żeby w liczniku nie znajdował się x. jak Ci się nie uda to Ci pomogę.

Eta: Czy funkcja miała być taka:

	−2x+3
f(x)=
	2x−1

bo niewyraźnie napisałeś

romuland: jednak Ci się uda

Eta:

Thor: eh, ledwo zaczne pisać juz rozwiązanie D

Pająk:

−2x+3
	tak, taka
2x−1

Eta: ok

Pająk: a jak ustalić te przedziały?

Gustlik: Do Ety i nie tylko: można prościej przekształcić tę funkcje − dzieląc licznik przez mianownik jak wielomiany. Nie trzeba wtedy wymyślać liczb pasujacych do mianownika. Nie wiem, jak Ty, ale ja nie jestem zwolennikiem kombinacyjnych metod, bo dla wielu uczniów sa one nieprzejrzyste. A tu jest proste dzielenie i te liczby same wyjdą.

−2x+3		2
	=−1+
2x−1		2x−1

−1 −−−−−−−−−−−−−−−−−−− (−2x+3):(2x−1) +2x−1 −−−−−−−−−−−−−−− = 2

Gustlik: Do Ety i nie tylko: można prościej przekształcić tę funkcje − dzieląc licznik przez mianownik jak wielomiany. Nie trzeba wtedy wymyślać liczb pasujacych do mianownika. Nie wiem, jak Ty, ale ja nie jestem zwolennikiem kombinacyjnych metod, bo dla wielu uczniów sa one nieprzejrzyste. A tu jest proste dzielenie i te liczby same wyjdą.

−2x+3		2
	=−1+
2x−1		2x−1

−1 −−−−−−−−−−−−−−−−−−− (−2x+3):(2x−1) +2x−1 −−−−−−−−−−−−−−− = 2

romuland: od −∞ do wyłączonego x z dziedziny, i od tego x do nieskończoności w jednym będzie malejąca a w drugim rosnąca w zależności w której ćwiartce się znajduje.

romuland: jak nie wiesz o co chodzi to zobacz sobie wykres hiperboli jak wygląda

Pająk: chyba raczej będzie tylko albo rosnąca albo malejąca?

Pająk: w końcu to hiperbola

Gustlik: Sorki, przypadkiem 2 razy kliknąłem, nie chcę spamować tego wątku.

romuland:

	1
TA będzie w pierwszej i 3 ćwiartce (a > 0 ) więc będzie malejąca (−∞ ,		) i rosnąca
	2

	1
(		, ∞)
	2

Eta: Gustlik Ja to wiem

Pająk: dlaczego rosnąca i malejąca?

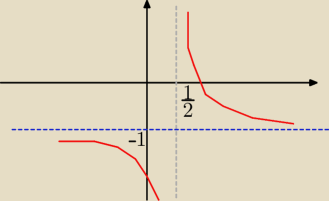
Eta: Tylko malejąca

	a
f(x) =		........ jest malejąca w całej dziedzinie gdy : a >0
	x

	a
f(x) =		........ jest rosnąca w całej dziedzinie gdy : a <0
	x

w tym przypadku a= 2 >0 co widzisz na wykresie

Magda: Jak wyznaczyć przedziały monotoniczności i ekstreme funkcji. f(x)= x⁴/4−2x²

xdc: Rozwiązujesz równania f'(x) = 0 i na podstawie znaku pochodnej w ustalasz przedziały monotoniczości (f'(x) < 0 f↘, f'(x) > 0 f↗). Dalej f''(x) = 0 i gdy f''(x) < 0 funkcja ma kształt ∩ gdy f''(x) > 0 to funkcja ma kształt ∪. Ekstrema to punty w których co się zmienia? Odpowiedź na to pytanie pozwoli Ci ustalić ekstrema funkcji.

Magda: Bardzo dziękuje